题目内容
6.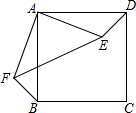 如图,将正方形ABCD中的△ADE绕着点A顺时针旋转与△ABF重合,若AE=4,则EF的长为4$\sqrt{2}$.
如图,将正方形ABCD中的△ADE绕着点A顺时针旋转与△ABF重合,若AE=4,则EF的长为4$\sqrt{2}$.
分析 旋转性可得AE=AF,∠DAE=∠BAF,进而可证明△EAF是等腰直角三角形,利用勾股定理即可求出EF.
解答 解:∵△ADE绕点A顺时针旋转至与△ABF重合,
∴AE=AF,∠DAE=∠BAF,
∵四边形ABCD是正方形,
∵∠DAE+∠BAE=90°,
∴∠BAF+∠BAE=90°,即∠FAE=90°,
∵AE=AF=4,
∴EF=$\sqrt{A{E}^{2}+A{F}^{2}}$=4$\sqrt{2}$.
故答案为:4$\sqrt{2}$.
点评 本题主要考查了旋转的性质,等腰直角三角形及正方形的性质.解题的关键是旋转前、后的图形全等.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
11.在0,-3,-1,5这四个数中,正数是( )
| A. | 0 | B. | -3 | C. | -1 | D. | 5 |
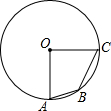 如图,已知A,B,C均在圆O上,且OA⊥OC,AB=1,BC=$\sqrt{2}$,则OABC的面积为$\frac{7}{4}$.
如图,已知A,B,C均在圆O上,且OA⊥OC,AB=1,BC=$\sqrt{2}$,则OABC的面积为$\frac{7}{4}$.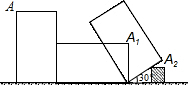 如图,小虎使一长为4cm,宽为2cm的长方形木板,在桌面上做无滑动的翻滚(顺时针方向)木板上点A位置变化为A→A1→A2,其中第二次翻滚被桌面上一小木块挡住,使木板与桌面成30°角.若连接AA2,则线段AA2的长(精确到0.1)约为( )
如图,小虎使一长为4cm,宽为2cm的长方形木板,在桌面上做无滑动的翻滚(顺时针方向)木板上点A位置变化为A→A1→A2,其中第二次翻滚被桌面上一小木块挡住,使木板与桌面成30°角.若连接AA2,则线段AA2的长(精确到0.1)约为( )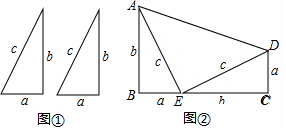
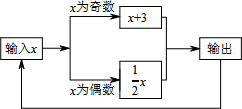 有一数值转换器,原理如图,若开始输入x的值是5,可发现第一次输出的结果是8,第二次输出的结果是4,…,请你探索第99次输出的结果是2.
有一数值转换器,原理如图,若开始输入x的值是5,可发现第一次输出的结果是8,第二次输出的结果是4,…,请你探索第99次输出的结果是2.