题目内容
20．
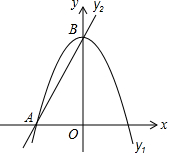如图，已知抛物线y1=-2x2+2与直线y2=2x+2交于A、B两点（1）求线段AB的长度；
（2）结合图象，请直接写出-2x2+2＞2x+2的解集．
分析 （1）直接求出两函数图象的交点进而得出AB的长；
（2）直接利用两函数的交点坐标得出不等式的解集即可．
解答 解：（1）∵抛物线y1=-2x2+2与直线y2=2x+2交于A、B两点，
∴-2x2+2=2x+2，
解得：x1=-1，x2=0，
当x=-1时，y=0，当x=0时，y=2，
故A（-1，0），B（0，2），
则AB=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$；
（2）由（1）得：-2x2+2＞2x+2的解集为：-1＜x＜0．
点评 此题主要考查了二次函数与不等式，正确得出两函数的交点坐标是解题关键．
练习册系列答案
相关题目
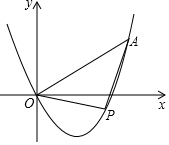如图，二次函数y=ax2-（4a-0.5）x（a＞0）的图象经过点A（4，m），若点P是这个二次函数图象上的一个动点，当△POA为等腰直角三角形时，a的值是$\frac{5}{6}$或$\frac{5}{4}$或$\frac{5}{12}$．
如图，AB=AC，AD=AE，CD=BE．求证：∠DAB=∠EAC．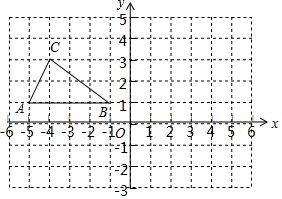
如图，在平面直角坐标系中，△ABC的顶点坐标分别为A（-5，1），B（-1，1），C（-4，3）．