题目内容
在Rt△ABC中,∠C=90°,AC=9,BC=12,则点C到斜边AB的距离是( )
(A) (B)
(B) (C)9 (D)6
(C)9 (D)6
【答案】A
【解析】
试题分析:根据题意画出相应的图形,如图所示,在Rt△ABC中,由AC及BC的长,利用勾股定理求出AB的长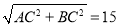 ,然后过C作CD⊥AB,由直角三角形的面积可以由两直角边乘积的一半来求,也可以由斜边AB乘以斜边上的高CD除以2来求,两者相等,即
,然后过C作CD⊥AB,由直角三角形的面积可以由两直角边乘积的一半来求,也可以由斜边AB乘以斜边上的高CD除以2来求,两者相等,即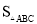 =
=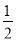 AC•BC=
AC•BC=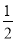 AB•CD,将AC,AB及BC的长代入求出CD的长
AB•CD,将AC,AB及BC的长代入求出CD的长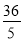 ,即为C到AB的距离.
,即为C到AB的距离.
故选A
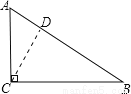
考点:勾股定理,三角形的面积
【题型】单选题
【结束】
4
已知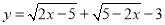 ,则2xy的值为
,则2xy的值为
A. -15 B. 15 C. -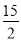 D.
D. 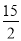
练习册系列答案
相关题目
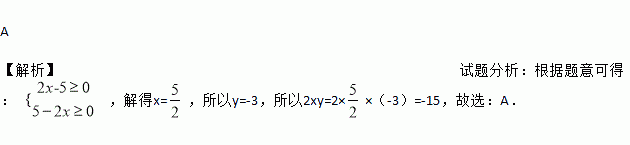

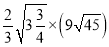
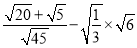 .
.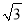 ;(2)1-
;(2)1-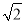
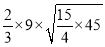 = 45
= 45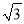 ;
;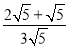 ﹣
﹣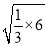 = 1﹣
= 1﹣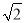 .
.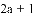
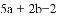
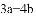
 B.
B. 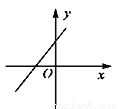 C.
C. 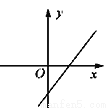 D.
D. 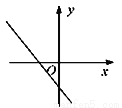
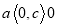 ,故选A.
,故选A.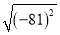 的算术平方根是____.
的算术平方根是____.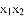 -
-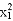 -
-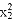 =-9,求实数k的值.
=-9,求实数k的值.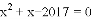 的不相等的两根,求a2+2a+b的值。
的不相等的两根,求a2+2a+b的值。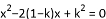 有实数根α、β,那么α+β的取值范围是( )
有实数根α、β,那么α+β的取值范围是( ) D. α+β≤
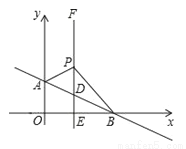
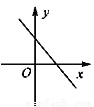
D. α+β≤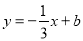 交y轴于点A(0,1),交x轴于点B.过点E(1,0)作x轴的垂线EF交AB于点D,P是直线EF上一动点,且在点D的上方,设P(1,n).
交y轴于点A(0,1),交x轴于点B.过点E(1,0)作x轴的垂线EF交AB于点D,P是直线EF上一动点,且在点D的上方,设P(1,n).