Question

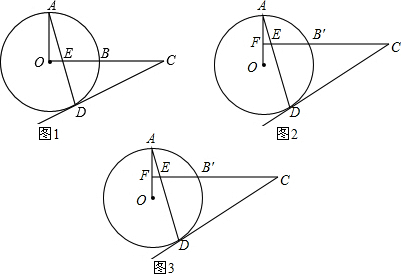
12．如图1，在菱形ABCD中，AC=2，BD=2$\sqrt{3}$，AC、BD相交于点O．
（1）AB的长为2；
（2）如图2，将一个足够大的直角三角板60°角的顶点放在菱形ABCD的顶点A处，绕点A左右旋转，其中三角板60°角的两边分别与边BC，CD相交于点E，F，连接EF与AC相交于点G．
①求证：△ABE≌△ACF；
②判断△AEF是哪一种特殊三角形，并说明理由．

Answer 1

分析 （1）利用菱形对角线互相垂直且平分可得AO、OB，根据勾股定理求出即可；
（2）①由（1）知，菱形ABCD的边长是2，AC=2，然后由△ABC和△ACD是等边三角形，利用ASA可证得△ABE≌△ACF；
②由①可得AE=AF，根据有一个角是60°的等腰三角形是等边三角形推出即可．

解答 解：（1）∵在菱形ABCD中，AC=2，BD=2$\sqrt{3}$，
∴∠AOB=90°，OA=$\frac{1}{2}$AC=1，BO=$\frac{1}{2}$BD=$\sqrt{3}$，
在Rt△AOB中，由勾股定理得：AB=$\sqrt{A{O}^{2}+B{O}^{2}}$=2；
故答案为：2；

（2）①∵由（1）知，菱形ABCD的边长是2，AC=2，
∴△ABC和△ACD是等边三角形，
∴∠BAC=∠BAE+∠CAE=60°，
∵∠EAF=∠CAF+∠CAE=60°，
∴∠BAE=∠CAF，
在△ABE和△ACF中，
$\left\{\begin{array}{l}{∠BAE=∠CAF}\\{AB=AC}\\{∠EBA=∠FCA}\end{array}\right.$，
∴△ABE≌△ACF（ASA），

②△AEF是等边三角形，
理由是：∵△ABE≌△ACF，
∴AE=AF，
∵∠EAF=60°，
∴△AEF是等边三角形．

点评 此题属于四边形的综合题．考查了菱形的性质，全等三角形的性质和判定，等边三角形的性质以及图形的旋转．解题的关键是掌握菱形菱形对角线互相垂直且平分．