题目内容
4. 如图,CE是△ABC的外角∠ACD的平分线,若∠B=40°,∠ACE=60°,则∠A=80度.
如图,CE是△ABC的外角∠ACD的平分线,若∠B=40°,∠ACE=60°,则∠A=80度.
分析 根据角平分线定义求出∠ACD,根据三角形的外角性质得出∠ACD=∠A+∠B,即可求出答案.
解答 解:∵∠ACE=60°,CE是△ABC的外角∠ACD的平分线,
∠ACD=2∠ACE=120°,
∵∠ACD=∠A+∠B,∠B=40°,
∴∠A=∠ACD-∠B=80°,
故答案为:80
点评 本题考查了三角形的外角性质的应用,能根据三角形的外角性质得出ACD=∠A+∠B是解此题的关键.

练习册系列答案
相关题目
11. 如图,甲、乙、丙、丁四个扇形的面积之比是1:2:3:4,则甲、乙、丙、丁四个扇形中圆心角度数最大的是( )度.
如图,甲、乙、丙、丁四个扇形的面积之比是1:2:3:4,则甲、乙、丙、丁四个扇形中圆心角度数最大的是( )度.
 如图,甲、乙、丙、丁四个扇形的面积之比是1:2:3:4,则甲、乙、丙、丁四个扇形中圆心角度数最大的是( )度.
如图,甲、乙、丙、丁四个扇形的面积之比是1:2:3:4,则甲、乙、丙、丁四个扇形中圆心角度数最大的是( )度.| A. | 36 | B. | 72 | C. | 144 | D. | 156 |
9.-$\frac{3}{4}$的倒数是( )
| A. | $\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | $-\frac{3}{4}$ | D. | $-\frac{4}{3}$ |
16.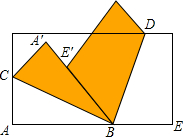 如图,将一张长方形纸片的角A、E分别沿着BC、BD折叠,点A落在A'处,点E落在边BA'上的E'处,则∠CBD的度数是( )
如图,将一张长方形纸片的角A、E分别沿着BC、BD折叠,点A落在A'处,点E落在边BA'上的E'处,则∠CBD的度数是( )
 如图,将一张长方形纸片的角A、E分别沿着BC、BD折叠,点A落在A'处,点E落在边BA'上的E'处,则∠CBD的度数是( )
如图,将一张长方形纸片的角A、E分别沿着BC、BD折叠,点A落在A'处,点E落在边BA'上的E'处,则∠CBD的度数是( )| A. | 85° | B. | 90° | C. | 95° | D. | 100° |
 如图,已知函数y=-2x+4的图象,观察图象回答下列问题:
如图,已知函数y=-2x+4的图象,观察图象回答下列问题:
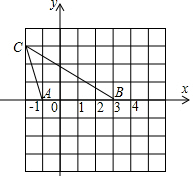 △ABC在平面直角坐标系中的位置如图所示,现另有一点D,满足以A,B,D为顶点的三角形与△ABC全等,则D点坐标为(4,3)或(-2,-3)或(4,-3).
△ABC在平面直角坐标系中的位置如图所示,现另有一点D,满足以A,B,D为顶点的三角形与△ABC全等,则D点坐标为(4,3)或(-2,-3)或(4,-3). 如图,已知线段a和∠1,用直尺和圆规作等腰△ABC,使AB=AC=a,∠B=∠1(不写作法,保留作图痕迹)
如图,已知线段a和∠1,用直尺和圆规作等腰△ABC,使AB=AC=a,∠B=∠1(不写作法,保留作图痕迹)