题目内容
13.已知关于x的方程x2+$\frac{1}{{x}^{2}}$+2(x+$\frac{1}{x}$)=6,那么x+$\frac{1}{x}$的值为-4或2..分析 由于x2+$\frac{1}{{x}^{2}}$=(x+$\frac{1}{x}$)2-2,所以原方程可变形为(x+$\frac{1}{x}$)2+2(x+$\frac{1}{x}$)-8=0,把x+$\frac{1}{x}$看成一个整体,解关于(x+$\frac{1}{x}$)的二元一次方程求出它的根.
解答 解:x2+$\frac{1}{{x}^{2}}$+2(x+$\frac{1}{x}$)=6,
所以x2+2+$\frac{1}{{x}^{2}}$+2(x+$\frac{1}{x}$)-8=0,
即(x+$\frac{1}{x}$)2+2(x+$\frac{1}{x}$)-8=0,
设x+$\frac{1}{x}$=y,则原式变形为y2+2y-8=0
解得,y1=-4,y2=2.
所以x+$\frac{1}{x}$=-4或x+$\frac{1}{x}$=2.
故答案为:-4或2.
点评 本题考查了完全平方公式、换元法和十字相乘法,把x2+$\frac{1}{{x}^{2}}$变形为(x+$\frac{1}{x}$)2-2,利用换元法是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图:P是?ABCD内的一点,S△APB:S△ABCD=1:3,则S△CPD:S△ABCD=1:6.
如图:P是?ABCD内的一点,S△APB:S△ABCD=1:3,则S△CPD:S△ABCD=1:6. 如图,CE是△ABC的外角∠ACD的平分线,若∠B=40°,∠ACE=60°,则∠A=80度.
如图,CE是△ABC的外角∠ACD的平分线,若∠B=40°,∠ACE=60°,则∠A=80度.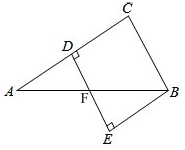 如图,△ABC中,AC的中垂线交AC、AB于点D、F,BE⊥DF交DF延长线于点E,若∠A=30°,BC=6,AF=BF,则四边形BCDE的面积是18$\sqrt{3}$.
如图,△ABC中,AC的中垂线交AC、AB于点D、F,BE⊥DF交DF延长线于点E,若∠A=30°,BC=6,AF=BF,则四边形BCDE的面积是18$\sqrt{3}$.