题目内容
4.用下列多边形不能单独铺满地面的是( )| A. | 正三角形 | B. | 正四边形 | C. | 正六边形 | D. | 正八边形 |
分析 分别求出正边形各内角的度数,看能否整除360°即可得出结论.
解答 解:A.正三角形每个内角为60°,能整除360°,所以能铺满地面;
B.正四边形每个内角为90°,能整除360°,所以能铺满地面;
C.正六边形每个内角为120°,能整除360°,所以能铺满地面;
D.正八边形每个内角为135°,不能整除360°,所以不能铺满地面;
故选D.
点评 此题考查了平面镶嵌(密铺),计算正多边形的内角能否整除360°是解答此题的关键.

练习册系列答案
相关题目
14.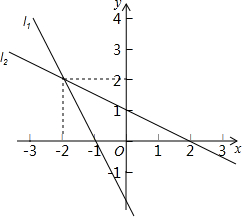 如图,直线l1的解析式为y1=k1x+b1,直线l2的解析式为y2=k2x+b2,则不等式k1x+b1>k2x+b2的解集是( )
如图,直线l1的解析式为y1=k1x+b1,直线l2的解析式为y2=k2x+b2,则不等式k1x+b1>k2x+b2的解集是( )
 如图,直线l1的解析式为y1=k1x+b1,直线l2的解析式为y2=k2x+b2,则不等式k1x+b1>k2x+b2的解集是( )
如图,直线l1的解析式为y1=k1x+b1,直线l2的解析式为y2=k2x+b2,则不等式k1x+b1>k2x+b2的解集是( )| A. | x>2 | B. | x<2 | C. | x>-2 | D. | x<-2 |
9.下列式子中,为最简二次根式的是( )
| A. | $\sqrt{10}$ | B. | $\sqrt{8}$ | C. | $\sqrt{\frac{1}{2}}$ | D. | $\frac{1}{{\sqrt{2}}}$ |
13.小颖随机抽样调查本班20名女同学所穿运动鞋尺码,并统计如表:
学校附近的商店经理根据表中决定本月多进尺码为23.0cm的女式运动鞋,商店经理的这一决定应用了哪个统计知识( )
| 尺码/cm | 21.5 | 22.0 | 22.5 | 23.0 | 23.5 |
| 人数 | 2 | 4 | 3 | 8 | 3 |
| A. | 众数 | B. | 中位数 | C. | 平均数 | D. | 方差 |
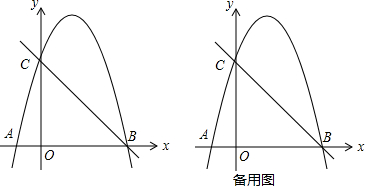 如图,已知抛物线y=ax2-3ax-4a(a≠0)与x轴交于A、B两点(A在B的左侧),与y轴交于点C,∠ACB=90°,点D 的坐标为(0,3)
如图,已知抛物线y=ax2-3ax-4a(a≠0)与x轴交于A、B两点(A在B的左侧),与y轴交于点C,∠ACB=90°,点D 的坐标为(0,3)