题目内容
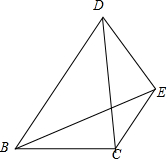 在△ABC中,BC=CD,∠BCD=90°,E是△BCD外一点,CE∥BD,且BE=BD,求
在△ABC中,BC=CD,∠BCD=90°,E是△BCD外一点,CE∥BD,且BE=BD,求| CE |
| BD |
考点:勾股定理
专题:
分析:作BM⊥CE,交EC的延长线于M,作CN⊥BD于N,根据平行线的性质和已知条件得出四边形BNCM是正方形,设CM=BM=BN=CN=DN=1,根据BE=BD,得出BE=BD=2,再根据勾股定理得出EM=
,从而求出CE=EM-CM=
-1,最后代入要求的式子即可得出答案.
| BE2-BM2 |
| 3 |
解答: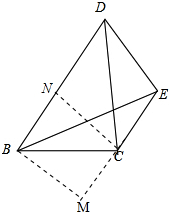 解:作BM⊥CE,交EC的延长线于M,作CN⊥BD于N,
解:作BM⊥CE,交EC的延长线于M,作CN⊥BD于N,
∵CE∥BD,
∴∠MCN=∠CND=90°,
∴四边形BNCM是矩形,
∵BC=CD,∠BCD=90°,
∴△BCD是等腰直角三角形,
∵CN⊥BD,
∴BN=DN=CN,
∴四边形BNCM是正方形,
设CM=BM=BN=CN=DN=1,
∵BE=BD,
则BE=BD=2,
∴EM=
=
,
∴CE=EM-CM=
-1,
∴
=
.
 解:作BM⊥CE,交EC的延长线于M,作CN⊥BD于N,
解:作BM⊥CE,交EC的延长线于M,作CN⊥BD于N,∵CE∥BD,
∴∠MCN=∠CND=90°,
∴四边形BNCM是矩形,
∵BC=CD,∠BCD=90°,
∴△BCD是等腰直角三角形,
∵CN⊥BD,
∴BN=DN=CN,
∴四边形BNCM是正方形,
设CM=BM=BN=CN=DN=1,
∵BE=BD,
则BE=BD=2,
∴EM=
| BE2-BM2 |
| 3 |
∴CE=EM-CM=
| 3 |
∴
| CE |
| BD |
| ||
| 2 |
点评:此题考查了勾股定理,用到的知识点是等腰直角三角形的判定与性质,平行线的性质,勾股定理,关键是作出辅助线,求出四边形BNCM是正方形.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
将多项式x2+4加上一个整式,使它成为完全平方式,则下列不满足条件的整式是( )
| A、-4 | ||
| B、±4x | ||
C、
| ||
D、
|
下列调查中,适宜采用普查的是( )
| A、了解宁德市空气质量情况 |
| B、了解闽江流域的水污染情况 |
| C、了解宁德市居民的环保意识 |
| D、了解全班同学每周体育锻炼的时间 |
 如图,四边形ABCD中,AE⊥BD,CF⊥BD,AE=CF,∠ADB=∠CBD.
如图,四边形ABCD中,AE⊥BD,CF⊥BD,AE=CF,∠ADB=∠CBD. 如图,数轴上表示1、
如图,数轴上表示1、 如图,数轴上表示1、
如图,数轴上表示1、