题目内容
11．
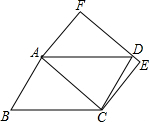如图，平行四边形ABCD和矩形ACEF的位置如图所示，点D在EF上，则平行四边形ABCD和矩形ACEF的面积S1、S2的大小关系是（ ）| A． | S1＞S2 | B． | S1=S2 | C． | S1＜S2 | D． | 3S1=2S2 |
分析 过D作DF⊥AC于F，根据平行四边形的判定得到四边形DFCE是矩形，于是得到DF=CE，根据矩形的面积公式和三角形的面积即可得到S1=S2．
解答 
解：过D作DF⊥AC于F，
∵四边形ACEF是矩形，
∴∠E=∠ECF=90°，
∴四边形DFCE是矩形，
∴DF=CE，
∵S1=2S△ACD=2×$\frac{1}{2}×AC•DF$=AC•DF，S2=AC•CE，
∴S1=S2，
故选B．
点评 本题考查了平行四边形的性质，矩形的性质以及平行四边形和矩形的面积的求法，正确的作出辅助线是解题的关键．
练习册系列答案
相关题目
1．在△ABC中，已知∠A=2∠B=3∠C，则三角形是（ ）
| A． | 锐角三角形 | B． | 直角三角形 | C． | 钝角三角形 | D． | 形状无法确定 |
19．
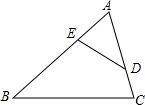如图，在△ABC中，∠B+∠CDE=∠C+∠BED，AE=2，AD=3，CD=1，则BE等于（ ）
如图，在△ABC中，∠B+∠CDE=∠C+∠BED，AE=2，AD=3，CD=1，则BE等于（ ）| A． | $\frac{3}{2}$ | B． | $\frac{2}{3}$ | C． | 2 | D． | 4 |
6．
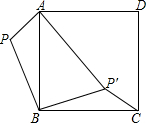如图，已知P为正方形ABCD外的一点，PA=1，PB=2，将△ABP绕点B顺时针旋转90°，使点P旋转至点P′，且AP′=3，则∠BP′C的度数为 （ ）
如图，已知P为正方形ABCD外的一点，PA=1，PB=2，将△ABP绕点B顺时针旋转90°，使点P旋转至点P′，且AP′=3，则∠BP′C的度数为 （ ）| A． | 105° | B． | 112.5° | C． | 120° | D． | 135° |
如图，点A，B，C，D在同一条直线上，△ABF≌△DCE，证明：AF∥DE．
3．
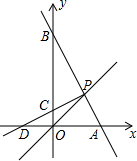如图，在平面直角坐标系中，直线y=x与直线y=-2x+3交于点P，直线y=-2x+3与x轴交于点A，与y轴交于B．
（1）求点P的坐标；
（2）过点P作PD⊥AB分别交x、y轴于D、C，求点C的坐标．
如图，在平面直角坐标系中，直线y=x与直线y=-2x+3交于点P，直线y=-2x+3与x轴交于点A，与y轴交于B．（1）求点P的坐标；
（2）过点P作PD⊥AB分别交x、y轴于D、C，求点C的坐标．
1．用m个正方形和n个正八边形铺设地面，则m、n满足的条件是（ ）
| A． | 2m+3n=8 | B． | 3m+2n=8 | C． | m+n=4 | D． | m+2n=6 |