题目内容
7. 如图,在矩形ABCD中,AB=4,AD=2.点P,Q同时从点A出发,点P以每秒2个单位的速度沿A→B→C→D的方向运动;点Q以每秒1个单位的速度沿A→D→C的方向运动,当P,Q两点相遇时,它们同时停止运动.设P,Q两点运动的时间为x(秒),△APQ的面积为S(平方单位).
如图,在矩形ABCD中,AB=4,AD=2.点P,Q同时从点A出发,点P以每秒2个单位的速度沿A→B→C→D的方向运动;点Q以每秒1个单位的速度沿A→D→C的方向运动,当P,Q两点相遇时,它们同时停止运动.设P,Q两点运动的时间为x(秒),△APQ的面积为S(平方单位).(1)点P,Q从出发到相遇所用的时间4秒.
(2)求S与x之间的函数关系式.
分析 (1)总路程除以总速度,就可以得到时间;
(2)根据三角形的面积公式和分段情况分别求出解析式.
解答 解:(1)(4×2+2×2)÷(2+1)=4.
故答案为:4;
(2)当0≤x≤2时,S=$\frac{1}{2}$•x•2x=x2.
当2<x≤3时,S=4×2-$\frac{1}{2}$×2×(x-2)-$\frac{1}{2}$×4×(2x-4)-$\frac{1}{2}$×(6-x)×(6-2x)=-x2+4x.
当3<x≤4时,S=$\frac{1}{2}$×2×(12-3x)=12-3x.
点评 本题考查了一元二次方程的应用,矩形的性质,以及函数的应用,本题关键知道分段来求.

练习册系列答案
相关题目
19.若ab≠1,且有5a2+2001a+9=0及9b2+2001b+5=0,则$\frac{a}{b}$的值是( )
| A. | $\frac{9}{5}$ | B. | $\frac{5}{9}$ | C. | $-\frac{2001}{5}$ | D. | $-\frac{2001}{9}$ |

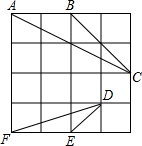 在4×4的正方形方格中,△ABC和△DEF的顶点都在边长为1的小正方形的顶点上.
在4×4的正方形方格中,△ABC和△DEF的顶点都在边长为1的小正方形的顶点上.