题目内容
19.若ab≠1,且有5a2+2001a+9=0及9b2+2001b+5=0,则$\frac{a}{b}$的值是( )| A. | $\frac{9}{5}$ | B. | $\frac{5}{9}$ | C. | $-\frac{2001}{5}$ | D. | $-\frac{2001}{9}$ |
分析 先把9b2+2001b+5=0变形为5•($\frac{1}{b}$)2+2001•$\frac{1}{b}$+9=0,则可把a、$\frac{1}{b}$为方程5x2+2001x+9=0的两根,然后根据根与系数的关系求解.
解答 解:∵9b2+2001b+5=0,
∴5•($\frac{1}{b}$)2+2001•$\frac{1}{b}$+9=0,
而5a2+2001a+9=0,
∴a、$\frac{1}{b}$为方程5x2+2001x+9=0的两根,
∴a•$\frac{1}{b}$=$\frac{9}{5}$.
故选A.
点评 本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
9.若a、b为有理数,下列说法正确的是( )
| A. | 若a≠b,则a2≠b2 | B. | 若a2=b2,则a=b | ||
| C. | 若a>b,则a2>b2 | D. | 若a、b不全为零,则a2+b2>0 |
 如图,在矩形ABCD中,AB=4,AD=2.点P,Q同时从点A出发,点P以每秒2个单位的速度沿A→B→C→D的方向运动;点Q以每秒1个单位的速度沿A→D→C的方向运动,当P,Q两点相遇时,它们同时停止运动.设P,Q两点运动的时间为x(秒),△APQ的面积为S(平方单位).
如图,在矩形ABCD中,AB=4,AD=2.点P,Q同时从点A出发,点P以每秒2个单位的速度沿A→B→C→D的方向运动;点Q以每秒1个单位的速度沿A→D→C的方向运动,当P,Q两点相遇时,它们同时停止运动.设P,Q两点运动的时间为x(秒),△APQ的面积为S(平方单位).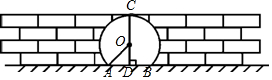 如图是某风景区的一个圆拱形门,路面AB宽为2米,净高5米,求圆拱形门所在圆的半径是多少米?
如图是某风景区的一个圆拱形门,路面AB宽为2米,净高5米,求圆拱形门所在圆的半径是多少米? 如图,在△ABC中,AB=AC,AD是角平分线,BE=CF,则下列说法:
如图,在△ABC中,AB=AC,AD是角平分线,BE=CF,则下列说法: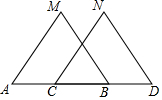 如图,已知MB=ND,∠MBA=∠NDC,如果∠M=∠N或∠A=∠NCD或AM∥CN或AB=CD,那么△ABM≌△CDN.
如图,已知MB=ND,∠MBA=∠NDC,如果∠M=∠N或∠A=∠NCD或AM∥CN或AB=CD,那么△ABM≌△CDN.