题目内容
2.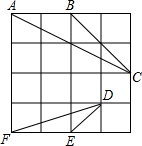 在4×4的正方形方格中,△ABC和△DEF的顶点都在边长为1的小正方形的顶点上.
在4×4的正方形方格中,△ABC和△DEF的顶点都在边长为1的小正方形的顶点上.(1)填空:∠ABC=135°,△ABC的面积为2.
(2)判断△ABC与△DEF是否相似,并说明理由.
(3)请在图中再画一个和△ABC相似但相似比不为1的格点三角形.
分析 (1)利用图形结合正方形的性质以及三角形面积公式得出即可;
(2)利用相似三角形的判定方法得出即可;
(3)将三角形的三边变为原来的$\frac{1}{2}$,进而得出答案.
解答 解:(1)由题意可得:∠ABC=90°+45°=135°,
△ABC的面积为=$\frac{1}{2}$×2×2=2;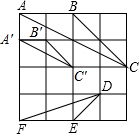 (2)相似,
(2)相似,
理由:∵AB=2BC=2$\sqrt{2}$,AC=2$\sqrt{5}$,DE=$\sqrt{2}$,EF=2,DF=$\sqrt{10}$,
∴$\frac{AB}{DE}$=$\frac{BC}{EF}$=$\frac{AC}{DF}$=$\sqrt{2}$,
∴△ABC∽△DEF;
(3)如图所示:△A′B′C′.
故答案为:135,2.
点评 此题主要考查了作图-相似变换,相似三角形的判定与性质,正确结合网格求出答案是解题关键.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
 如图,已知一次函数y=ax+b的图象为直线l,则关于x的不等式ax+b<0的解集为x>2.
如图,已知一次函数y=ax+b的图象为直线l,则关于x的不等式ax+b<0的解集为x>2.
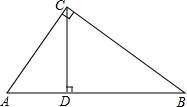 如图,△ABC为直角三角形,∠ACB=90°,CD为斜边AB上的高,D为垂足,△ABC∽△ACD∽△CBD,那么下列等式:①AC2=AD•AB;②CD2=AD•BD;③BC2=BD•AB;④AC•CB=BA•CD,其中正确的有①②③④.(填序号)
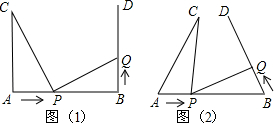
如图,△ABC为直角三角形,∠ACB=90°,CD为斜边AB上的高,D为垂足,△ABC∽△ACD∽△CBD,那么下列等式:①AC2=AD•AB;②CD2=AD•BD;③BC2=BD•AB;④AC•CB=BA•CD,其中正确的有①②③④.(填序号) 如图,在矩形ABCD中,AB=4,AD=2.点P,Q同时从点A出发,点P以每秒2个单位的速度沿A→B→C→D的方向运动;点Q以每秒1个单位的速度沿A→D→C的方向运动,当P,Q两点相遇时,它们同时停止运动.设P,Q两点运动的时间为x(秒),△APQ的面积为S(平方单位).
如图,在矩形ABCD中,AB=4,AD=2.点P,Q同时从点A出发,点P以每秒2个单位的速度沿A→B→C→D的方向运动;点Q以每秒1个单位的速度沿A→D→C的方向运动,当P,Q两点相遇时,它们同时停止运动.设P,Q两点运动的时间为x(秒),△APQ的面积为S(平方单位).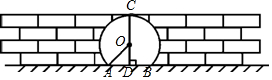 如图是某风景区的一个圆拱形门,路面AB宽为2米,净高5米,求圆拱形门所在圆的半径是多少米?
如图是某风景区的一个圆拱形门,路面AB宽为2米,净高5米,求圆拱形门所在圆的半径是多少米?