题目内容
13.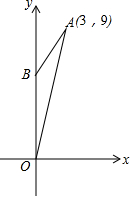 在图中,A(3,9)是直角坐标平面上的一点,而B是y轴上的一点,使OB=AB.
在图中,A(3,9)是直角坐标平面上的一点,而B是y轴上的一点,使OB=AB.(a)求B的坐标.
(b)求△OAB的面积.
分析 (1)作辅助线,设AB=OB=x,则BC=9-x,根据勾股定理列方程可求x的值,写出B的坐标;
(2)直接代入三角形面积公式计算即可.
解答 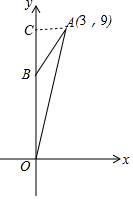 解:(1)过A作AC⊥y轴于C,
解:(1)过A作AC⊥y轴于C,
∵A(3,9),
∴AC=3,OC=9,
设AB=OB=x,则BC=9-x,
在Rt△ACB中,由勾股定理得:AC2+BC2=AB2,
32+(9-x)2=x2,
x=5,
∴OB=5,
∴B(0,5);
(2)S△AOB=$\frac{1}{2}$OB•AC=$\frac{1}{2}$×5×3=$\frac{15}{2}$.
点评 本题考查了图形与点的坐标特点、勾股定理、三角形的面积,熟练掌握点的坐标与图形特点是关键,注意利用数形结合的思想.

练习册系列答案
相关题目
3.下列判断不正确的是( )
| A. | 如果$\overrightarrow{AB}$=$\overrightarrow{CD}$,那么|$\overrightarrow{AB}$|=|$\overrightarrow{CD}$| | B. | $\overrightarrow{a}$+$\overrightarrow{b}$=$\overrightarrow{b}$+$\overrightarrow{a}$ | ||
| C. | 如果非零向量$\overrightarrow{a}$=k•$\overrightarrow{b}$(k≠0),那么$\overrightarrow{a}$∥$\overrightarrow{b}$ | D. | $\overrightarrow{AB}$+$\overrightarrow{BA}$=0 |
18.一项工程,甲单独做a小时完成,乙单独做b小时完成,甲、乙两人一起完成这项工程所需时间为( )
| A. | $\frac{ab}{a+b}$小时 | B. | $\frac{a+b}{ab}$小时 | C. | a+b小时 | D. | $\frac{1}{a+b}$小时 |
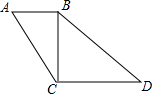
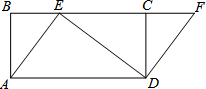 如图,四边形ABCD是矩形,点E在BC边上,点F在BC延长线上,且∠CDF=∠BAE,求证:四边形AEFD是平行四边形.
如图,四边形ABCD是矩形,点E在BC边上,点F在BC延长线上,且∠CDF=∠BAE,求证:四边形AEFD是平行四边形.
 已知,如图,∠ABC=∠BCD=90°,AC=15,sinA=$\frac{4}{5}$,BD=20,求∠D的三个三角函数值.
已知,如图,∠ABC=∠BCD=90°,AC=15,sinA=$\frac{4}{5}$,BD=20,求∠D的三个三角函数值. 如图,在△ABC中,AB=1,AC=2,现将△ABC绕点C顺时针旋转90°得到△A′B′C′,连接AB′,并有AB′=3,求∠B′A′C的大小.
如图,在△ABC中,AB=1,AC=2,现将△ABC绕点C顺时针旋转90°得到△A′B′C′,连接AB′,并有AB′=3,求∠B′A′C的大小.