题目内容
1.若关于x的一元二次方程x2+4x+k-1=0有两个不相等的实数根.(1)求k的取值范围;
(2)若该方程的两个实数根的积为2,求k的值.
分析 (1)由方程有两个不相等的实数根,结合根的判别式即可得出△=20-4k>0,解之即可得出k的取值范围;
(2)由根与系数的关系结合该方程的两个实数根的积为2,即可得出k-1=2,解之即可求出k值.
解答 解:(1)∵方程x2+4x+k-1=0有两个不相等的实数根,
∴△=42-4(k-1)=20-4k>0,
解得:k<5.
(2)设方程的两个根分别为m、n,
根据题意得:mn=k-1=2,
解得:k=3.
点评 本题考查了根与系数的关系以及根的判别式,解题的关键是:(1)熟练掌握“当△>0时,方程有两个不相等的实数根”;(2)牢记两根之积等于$\frac{c}{a}$.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
11.李克强总理在2017年政府工作报告中指出:“完善就业政策,加大就业培训力度,加强对灵活就业、新就业形态的支持,今年高校毕业生7950000人,再创历史新高,要实施好就业促进、创业引领、基层成长等计划,促进多渠道就业创业.”其中数据7950000用科学记数法表示是( )
| A. | 795×104 | B. | 7.95×105 | C. | 0.795×107 | D. | 7.95×106 |
9.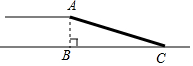 长清区政府准备在大学城修建一座高AB=6m的过街天桥,已知天桥的坡面AC与地面BC的夹角∠ACB的正弦值为$\frac{1}{3}$,则坡面AC的长度为( )m.
长清区政府准备在大学城修建一座高AB=6m的过街天桥,已知天桥的坡面AC与地面BC的夹角∠ACB的正弦值为$\frac{1}{3}$,则坡面AC的长度为( )m.
 长清区政府准备在大学城修建一座高AB=6m的过街天桥,已知天桥的坡面AC与地面BC的夹角∠ACB的正弦值为$\frac{1}{3}$,则坡面AC的长度为( )m.
长清区政府准备在大学城修建一座高AB=6m的过街天桥,已知天桥的坡面AC与地面BC的夹角∠ACB的正弦值为$\frac{1}{3}$,则坡面AC的长度为( )m.| A. | 16 | B. | 10 | C. | 18 | D. | 8$\sqrt{3}$ |
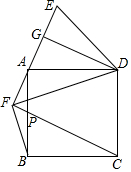 如图,正方形ABCD,过A作直线AE,作DG⊥AE,AG=GE,连接DE.
如图,正方形ABCD,过A作直线AE,作DG⊥AE,AG=GE,连接DE.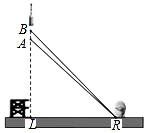 2016年11月3日,我国第一枚大型运载火箭“长征5号”在海南文昌航天发射场顺利升空,这标志着我国从航天大国迈向航天强国.如图,火箭从地面L处发射,当火箭到达A点时,从位于地面R处雷达站测得AR的距离是6km,仰角为42.4°;1秒后火箭到达B点,此时测得仰角为45.5°.
2016年11月3日,我国第一枚大型运载火箭“长征5号”在海南文昌航天发射场顺利升空,这标志着我国从航天大国迈向航天强国.如图,火箭从地面L处发射,当火箭到达A点时,从位于地面R处雷达站测得AR的距离是6km,仰角为42.4°;1秒后火箭到达B点,此时测得仰角为45.5°.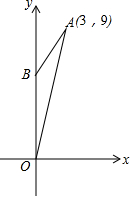 在图中,A(3,9)是直角坐标平面上的一点,而B是y轴上的一点,使OB=AB.
在图中,A(3,9)是直角坐标平面上的一点,而B是y轴上的一点,使OB=AB.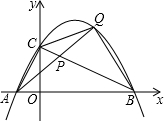 如图,抛物线y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2与x轴交于点A,B,与y轴交于点C.点P是线段BC上的动点(点P不与B,C重合),连接并延长AP交抛物线于另一点Q,设点Q的横坐标为x.
如图,抛物线y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2与x轴交于点A,B,与y轴交于点C.点P是线段BC上的动点(点P不与B,C重合),连接并延长AP交抛物线于另一点Q,设点Q的横坐标为x.