题目内容
10．
如图所示，MN为⊙O的弦，∠N=50°，则∠MON的度数为（ ）??
| A． | 40° | B． | 50°? | C． | 80° | D． | 100° |
分析 根据半径相等得到OM=ON，则∠M=∠N=50°，然后根据三角形内角和定理计算∠MON的度数．
解答 解：∵OM=ON，
∴∠M=∠N=50°，
∴∠MON=180°-2×50°=80°．
故选C．
点评 本题考查了圆的认识：掌握与圆有关的概念（弦、直径、半径、弧、半圆、优弧、劣弧、等圆、等弧等）．
练习册系列答案
相关题目
1．下列说法错误的是（ ）
| A． | 抛物线y=2x2的图象向左平移2个单位，再向下平移1个单位，则所得抛物线的解析式为y=2x2-8x+7 | |
| B． | 方程-x2+bx+c=0无实数根，则二次函数y=-x2+bx+c的图象一定在x轴下方 | |
| C． | 将长度为1m的木条黄金分割，较短的一段木条长为$\frac{{3-\sqrt{5}}}{2}$m | |
| D． | 两个等腰直角三角形一定相似 |
18．抛物线y=x2-8x+9的顶点坐标为（ ）
| A． | （4，7） | B． | （-4，7） | C． | （4，-7） | D． | （-4，-7） |
如图是一名考古学家发现的一块古代车轮碎片，你能帮他找到这个车轮的半径吗？（画出示意图，保留作图痕迹）
2．某种新产品的进价是120元，在试销阶段发现产品的日销售量y（件）与每件售价x（元）存在一次函数关系，部分对应值如下表：
（1）请你根据表中所给数据直接写出日销售量y（件）与每件售价x（元）之间的关系式：y=-x+200，自变量x的取值范围是x≥120
（2）在不改变上述关系的情况下，请你帮助商场经理策划每件商品定价为多少元时，每日盈利可达到1600元．
| 日销售量y（件） | 70 | 50 | 35 |
| 每件售价x（元） | 130 | 150 | 165 |
（2）在不改变上述关系的情况下，请你帮助商场经理策划每件商品定价为多少元时，每日盈利可达到1600元．
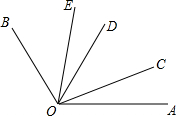如图，OC，OD，OE是∠AOB内部的三条射线，下面关于∠EOC的表述：①∠EOC=∠BOC-∠BOE；②∠EOC=∠EOD+∠COD；③∠EOC=∠BOC+∠AOE-∠AOB；④∠EOC=∠AOB-∠BOD，其中表述正确的个数有（ ）