题目内容
15.若抛物线y=ax2+2与抛物线y=-3x2-2关于原点对称,则a=3.分析 直接根据平面直角坐标系中,点关于原点对称的特点得出答案.
解答 解:抛物线y=-3x2-2关于原点对称的抛物线x、y均互为相反数,得-y=-3(-x)2-2=-3x2-2,即y=3x2+2,
所以,抛物线y=ax2+2中的a=3.
故答案为3.
点评 本题考查了二次函数图象与几何变换.需要掌握点与函数的关系,还有点的对称性问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.如果x+3y=2003,那么[(x2+2xy-3y2)-4006(x-y)]÷(x-y)的值是( )
| A. | 2003 | B. | -2003 | C. | 4006 | D. | 不能确定 |
6.下列各对数中,数值相等的是( )
| A. | -33和(-3)3 | B. | -32和(-3)2 | C. | (-2)3和(-3)2 | D. | -3×23和(-3×2)3 |
10. 如图所示,MN为⊙O的弦,∠N=50°,则∠MON的度数为( )?
如图所示,MN为⊙O的弦,∠N=50°,则∠MON的度数为( )?
?
 如图所示,MN为⊙O的弦,∠N=50°,则∠MON的度数为( )?
如图所示,MN为⊙O的弦,∠N=50°,则∠MON的度数为( )??
| A. | 40° | B. | 50°? | C. | 80° | D. | 100° |
4.函数y=3x2-1的图象向上平移两个单位后表示的函数关系式为( )
| A. | y=3x2+1 | B. | y=3x2-3 | C. | y=3(x+2)2-1 | D. | y=3(x-2)2-1 |
5.若y=ax2+bx+c是关于x的二次函数且a为整数,并且不等式4x≤ax2+bx+c≤2(x2+1)在实数范围内恒成立,则二次函数的解析式为( )
| A. | y=x2+2x+1 | B. | y=x2+2x+2 | C. | y=2x2+2x+1 | D. | y=2x2+2x+2 |
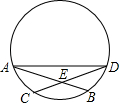 如图,弦AB=CD,AB与CD相交于点E,求证:(1)$\widehat{AC}$=$\widehat{BD}$;(2)AE=DE.
如图,弦AB=CD,AB与CD相交于点E,求证:(1)$\widehat{AC}$=$\widehat{BD}$;(2)AE=DE.