题目内容
10. 如图,在矩形ABCD中,AB=5,BC=7,点E为BC上一动点,把△ABE沿AE折叠,当点B的对应点B′落在∠ADC的角平分线上时,则点B′到BC的距离为2或1.
如图,在矩形ABCD中,AB=5,BC=7,点E为BC上一动点,把△ABE沿AE折叠,当点B的对应点B′落在∠ADC的角平分线上时,则点B′到BC的距离为2或1.
分析 连接B′D,过点B′作B′M⊥AD于M.设DM=B′M=x,则AM=7-x,根据等腰直角三角形的性质和折叠的性质得到:(7-x)2=25-x2,通过解方程求得x的值,易得点B′到BC的距离.
解答 解: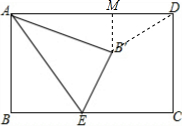 连接B′D,过点B′作B′M⊥AD于M.
连接B′D,过点B′作B′M⊥AD于M.
∵点B的对应点B′落在∠ADC的角平分线上,
∴设DM=B′M=x,则AM=7-x,
又由折叠的性质知AB=AB′=5,
∴在直角△AMB′中,由勾股定理得到:AM2=AB′2-B′M2
即(7-x)2=25-x2,
解得x=3或x=4,
则点B′到BC的距离为2或1.
故答案为:2或1.
点评 本题考查的是翻折变换的性质,掌握翻折变换是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等是解题的关键.

练习册系列答案
相关题目
20.函数y=$\frac{2}{x}$(y>0)与y=2x(y>0)的交点坐标为( )
| A. | (1,2) | B. | (1,-2) | C. | (-1,2) | D. | (-1,-2) |
1.圣诞节期间,艾艾妈妈经营的礼品店购进一大袋除颜色外其余都相同的散装玻璃球1500,艾艾将袋子中的玻璃球搅匀后,从中随机摸出一颗并记下颜色,然后放回,搅匀后再随机摸出一颗并记下颜色,再放回…多次重复上述过程后,艾艾发现摸到紫色玻璃球的频率逐渐稳定在0.15,由此可估计大袋中约有紫色玻璃球( )
| A. | 200颗 | B. | 225颗 | C. | 250颗 | D. | 无法确定 |
5.下列关系式中,正确的是( )
| A. | (b+a)2=b2-2ab+a2 | B. | (b+a)(b-a)=b2-a2 | C. | (b-a)2=b2-a 2 | D. | (a+b)(-a-b)=a2-b2 |
15.下列各数是无理数的是( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\sqrt{4}$ | C. | $\sqrt{{4}^{-2}}$ | D. | $\root{3}{-8}$ |
19.若等腰三角形底角为70°,则这个等腰三角形的顶角为( )
| A. | 110° | B. | 70° | C. | 40° | D. | 55° |
 如图,将四边形ABCD绕原点O旋转180°得四边形A′B′C′D′.
如图,将四边形ABCD绕原点O旋转180°得四边形A′B′C′D′.