题目内容
15.如果点A(m,n)、B(m-1,n-2)均在一次函数y=kx+b(k≠0)的图象上,那么k的值为( )| A. | 2 | B. | 1 | C. | -1 | D. | -2 |
分析 由点A、B的坐标结合一次函数图象上点的坐标特,可得出关于k、b的二元一次方程组,解之即可得出k值.
解答 解:∵点A(m,n)、B(m-1,n-2)均在一次函数y=kx+b(k≠0)的图象上,
∴$\left\{\begin{array}{l}{n=mk+b}\\{n-2=(m-1)k+b}\end{array}\right.$,
解得:k=2.
故选A.
点评 本题考查了一次函数图象上点的坐标特征,牢记“直线上任意一点的坐标都满足函数关系式y=kx+b”是解题的关键.

练习册系列答案
相关题目
3.从分别写有数字-4、-3、-2、-1、0、1、2、3、4的九张一样的卡片中,任意抽取一张卡片,则所抽卡片上数字的绝对值小于2<“m“:math xmlns:dsi='http://www.dessci.com/uri/2003/MathML'dsi:zoomscale='150'dsi:_mathzoomed='1'style='CURSOR:pointer; DISPLAY:inline-block'>2$\sqrt{2}$的概率是( )
| A. | $\frac{1}{9}$ | B. | $\frac{1}{3}$ | C. | $\frac{5}{9}$ | D. | $\frac{2}{3}$ |
7.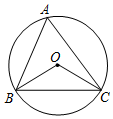 如图,⊙O是△ABC的外接圆,连接OB、OC,若⊙O的半径为2,∠BAC=60°,则BC的长为( )
如图,⊙O是△ABC的外接圆,连接OB、OC,若⊙O的半径为2,∠BAC=60°,则BC的长为( )
 如图,⊙O是△ABC的外接圆,连接OB、OC,若⊙O的半径为2,∠BAC=60°,则BC的长为( )
如图,⊙O是△ABC的外接圆,连接OB、OC,若⊙O的半径为2,∠BAC=60°,则BC的长为( )| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 4 | D. | 4$\sqrt{3}$ |
5.一组数据8,3,8,6,7,8,7的众数和极差分别是( )
| A. | 8,3 | B. | 8,5 | C. | 7,8 | D. | 8,7 |
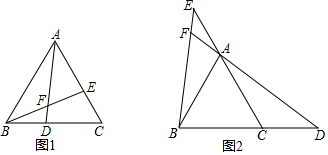 已知等边△ABC中,D,E分别是边BC,AC所在直线上的两点,且BD=CE,直线AD,BE交于点F.
已知等边△ABC中,D,E分别是边BC,AC所在直线上的两点,且BD=CE,直线AD,BE交于点F. 如图,AB=AC,BD=CD,若∠B=30°,∠BDC=100°,则∠A=40°.
如图,AB=AC,BD=CD,若∠B=30°,∠BDC=100°,则∠A=40°. 如图,在⊙O中,已知∠BAC=∠CDA=20°,则∠ABO的度数为50°.
如图,在⊙O中,已知∠BAC=∠CDA=20°,则∠ABO的度数为50°.
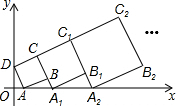 在平面直角坐标系中,正方形ABCD的位置如右图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1,作正方形A1B1C1C;延长C1B1交x轴于点A2,作正方形A2B2C2C1,…按这样的规律进行下去,第2017个正方形的面积为5×($\frac{3}{2}$)4032.
在平面直角坐标系中,正方形ABCD的位置如右图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1,作正方形A1B1C1C;延长C1B1交x轴于点A2,作正方形A2B2C2C1,…按这样的规律进行下去,第2017个正方形的面积为5×($\frac{3}{2}$)4032.