题目内容
2.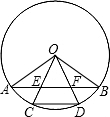 如图,OA、OB是⊙O的两条半径,且OA⊥OB,C、D是$\widehat{AB}$的三等两点,OC、OD分别交AB于E、F,则AE、CD与BF相等吗?为什么?
如图,OA、OB是⊙O的两条半径,且OA⊥OB,C、D是$\widehat{AB}$的三等两点,OC、OD分别交AB于E、F,则AE、CD与BF相等吗?为什么?
分析 由于C、D是弧AB的三等分点,易得∠AOC=∠DOB,又OA=OB=OC,易证得△AOC≌△OCD,可得∠ACO=∠OCD,易知∠AEC=∠OCD,因此∠ACO=∠AEC,即AC=AE=BF.
解答 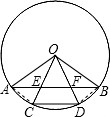 解:CD=AE=BF.
解:CD=AE=BF.
理由:连接AC、BD,
∵C,D是$\widehat{AB}$的三等分点,
∴AC=CD=BD,
∵∠AOC=∠COD,OA=OC=OD,
∴△ACO≌△DCO.
∴∠ACO=∠OCD.
∵OA⊥OB,
∴∠AOC=∠COD=∠BOD=30°,∠OAB=∠OBA=45°,
∴∠OEF=∠OAE+∠AOE=45°+30°=75°,∠OCD=$\frac{180°-30°}{2}$=75°,
∴∠OEF=∠OCD,
∴CD∥AB,
∴∠AEC=∠OCD,
∴∠ACO=∠AEC.
∴AC=AE,
同理,BF=BD.
又∵AC=CD=BD
∴CD=AE=BF.
点评 本题主要考查了全等三角形的判定和性质、圆周角定理、等腰三角形的性质等知识的综合应用能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
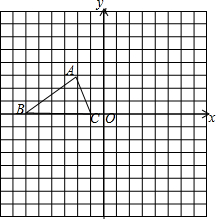 如图,已知△ABC的三个顶点的坐标分别为A(-2,3)、B(-6,0)、C(-1,0).
如图,已知△ABC的三个顶点的坐标分别为A(-2,3)、B(-6,0)、C(-1,0).