题目内容
2. 如图,Rt△ABC中,∠C=90°,BC=6,AC=8,D、E分别为AC、AB的中点,连接DE,则△ADE的面积是6.
如图,Rt△ABC中,∠C=90°,BC=6,AC=8,D、E分别为AC、AB的中点,连接DE,则△ADE的面积是6.
分析 根据题意求出AD、DE,根据三角形中位线定理得到DE∥BC,根据三角形的面积公式计算即可.
解答 解:∵D、E分别为AC、AB的中点,
∴AD=$\frac{1}{2}$AC=4,DE=$\frac{1}{2}$BC=3,DE∥BC,
∴∠ADE=∠C=90°,
∴△ADE的面积=$\frac{1}{2}$×AD×DE=6,
故答案为:6.
点评 本题考查的是三角形的中位线定理的应用,掌握三角形的中位线平行于第三边,且等于第三边的一半是解题的关键.

练习册系列答案
相关题目
13.已知关于x,y的二元一次方程组$\left\{\begin{array}{l}{3x+2y=a+2}\\{2x+3y=a}\end{array}\right.$的解满足x与y之和为2,求a的值.
10.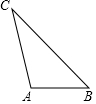 如图,△ABC是一块三条边长均不相等的薄板,要在△ABC薄板中裁剪出一个面积最大的圆形薄板,则圆形薄板的圆心应是△ABC的( )
如图,△ABC是一块三条边长均不相等的薄板,要在△ABC薄板中裁剪出一个面积最大的圆形薄板,则圆形薄板的圆心应是△ABC的( )
 如图,△ABC是一块三条边长均不相等的薄板,要在△ABC薄板中裁剪出一个面积最大的圆形薄板,则圆形薄板的圆心应是△ABC的( )
如图,△ABC是一块三条边长均不相等的薄板,要在△ABC薄板中裁剪出一个面积最大的圆形薄板,则圆形薄板的圆心应是△ABC的( )| A. | 三条高的交点 | B. | 三条中线的交点 | ||
| C. | 三边垂直平分线的交点 | D. | 三个内角角平分线的交点 |
17.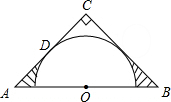 如图,在△ABC中,∠C=90°,AC=BC,AB=2,点O为AB的中点,以点O为圆心作半圆与边AC相切于点D.则图中阴影部分的面积为( )
如图,在△ABC中,∠C=90°,AC=BC,AB=2,点O为AB的中点,以点O为圆心作半圆与边AC相切于点D.则图中阴影部分的面积为( )
 如图,在△ABC中,∠C=90°,AC=BC,AB=2,点O为AB的中点,以点O为圆心作半圆与边AC相切于点D.则图中阴影部分的面积为( )
如图,在△ABC中,∠C=90°,AC=BC,AB=2,点O为AB的中点,以点O为圆心作半圆与边AC相切于点D.则图中阴影部分的面积为( )| A. | 1-$\frac{1}{4}$π | B. | $\frac{1}{2}$-$\frac{π}{8}$ | C. | 2-$\frac{3π}{4}$ | D. | 2-$\frac{1}{4}$π |
14.关于x的一元二次方程(a+1)x2-x+a2-2a-2=0,有一个根是1,则a=( )
| A. | -1 | B. | 2 | C. | 2或-1 | D. | -2或1 |
11.下列各式化简后的结果为3$\sqrt{2}$的是( )
| A. | $\sqrt{6}$ | B. | $\sqrt{12}$ | C. | $\sqrt{18}$ | D. | $\sqrt{36}$ |
12. 如图,AB∥CD,E为CD上一点,射线EF经过点A,EC=EA.若∠CAE=30°,则∠BAF=( )
如图,AB∥CD,E为CD上一点,射线EF经过点A,EC=EA.若∠CAE=30°,则∠BAF=( )
 如图,AB∥CD,E为CD上一点,射线EF经过点A,EC=EA.若∠CAE=30°,则∠BAF=( )
如图,AB∥CD,E为CD上一点,射线EF经过点A,EC=EA.若∠CAE=30°,则∠BAF=( )| A. | 30° | B. | 40° | C. | 50° | D. | 60° |
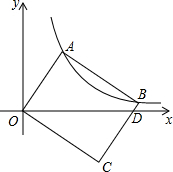 如图,在平面直角坐标系xOy,矩形OABC的顶点A、B在双曲线y=$\frac{k}{x}$(x>0)上.若点A的坐标为(1,2),则点B坐标为(4,$\frac{1}{2}$).
如图,在平面直角坐标系xOy,矩形OABC的顶点A、B在双曲线y=$\frac{k}{x}$(x>0)上.若点A的坐标为(1,2),则点B坐标为(4,$\frac{1}{2}$).