题目内容
已知二次函数y=ax2+bx+c的图象与x轴交于点(1,0)和(2,0),且过点(3,4).
(1)求二次函数的表达式;
(2)求顶点坐标;
(3)x取什么值时,y随x的增大而增大?x取什么值时,y随x增大而减少?
(1)求二次函数的表达式;
(2)求顶点坐标;
(3)x取什么值时,y随x的增大而增大?x取什么值时,y随x增大而减少?
考点:抛物线与x轴的交点
专题:
分析:(1)设二次函数解析式为y=a(x-1)(x-2),然后把点(3,4)代入函数解析式求得a的值即可;
(2)将(1)中抛物线的解析式利用配方法转化为顶点式,可以直接写出顶点坐标;
(3)根据抛物线的开口方向和对称轴写出答案.
(2)将(1)中抛物线的解析式利用配方法转化为顶点式,可以直接写出顶点坐标;
(3)根据抛物线的开口方向和对称轴写出答案.
解答: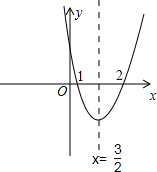 解:(1)∵二次函数y=ax2+bx+c的图象与x轴交于点(1,0)和(2,0),
解:(1)∵二次函数y=ax2+bx+c的图象与x轴交于点(1,0)和(2,0),
∴设该二次函数解析式为y=a(x-1)(x-2)(a≠0),
把点(3,4)代入,得
a(3-1)(3-2)=4,
解得 a=2.
则该抛物线的解析式为:y=2(x-1)(x-2);
(2)由(1)知,抛物线的解析式为y=2(x-1)(x-2).
∵y=2(x-1)(x-2)=2(x-
)2-
.
∴该抛物线的顶点坐标是:(
,-
).
(3)由抛物线的解析式y=2(x-
)2-
知,抛物线开口方向向上,对称轴是x=
.
结合二次函数y=ax2+bx+c的图象与x轴交于点(1,0)和(2,0),作出该抛物线的大致图象.
如图所示,在当x>
时,y随x的增大而增大;当x<
时,y随x的增大而减小.
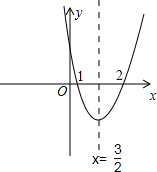 解:(1)∵二次函数y=ax2+bx+c的图象与x轴交于点(1,0)和(2,0),
解:(1)∵二次函数y=ax2+bx+c的图象与x轴交于点(1,0)和(2,0),∴设该二次函数解析式为y=a(x-1)(x-2)(a≠0),
把点(3,4)代入,得
a(3-1)(3-2)=4,
解得 a=2.
则该抛物线的解析式为:y=2(x-1)(x-2);
(2)由(1)知,抛物线的解析式为y=2(x-1)(x-2).
∵y=2(x-1)(x-2)=2(x-
| 3 |
| 2 |
| 1 |
| 2 |
∴该抛物线的顶点坐标是:(
| 3 |
| 2 |
| 1 |
| 2 |
(3)由抛物线的解析式y=2(x-
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
结合二次函数y=ax2+bx+c的图象与x轴交于点(1,0)和(2,0),作出该抛物线的大致图象.
如图所示,在当x>
| 3 |
| 2 |
| 3 |
| 2 |
点评:本题考查了抛物线与x轴的交点.解题时,需要熟悉抛物线解析式的三种形式,并且掌握抛物线的性质.

练习册系列答案
 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
 如图,在△ABC中,DE∥BC,AD=1,AB=3,DE=2,则BC的长是( )
如图,在△ABC中,DE∥BC,AD=1,AB=3,DE=2,则BC的长是( )| A、2 | B、4 | C、6 | D、8 |
 如图,A,B,C是⊙O的三等分点,A,D,E,F,G是⊙O的五等分点,求证:BE是⊙O的内接正十五边形的一边.
如图,A,B,C是⊙O的三等分点,A,D,E,F,G是⊙O的五等分点,求证:BE是⊙O的内接正十五边形的一边. 如图,在Rt△ABC中,∠BAC=90°,过顶点A的直线DE∥BC,∠ABC,∠ACB的平分线分别交DE于点E、D,若AC=3,BC=5,则DE的长为( )
如图,在Rt△ABC中,∠BAC=90°,过顶点A的直线DE∥BC,∠ABC,∠ACB的平分线分别交DE于点E、D,若AC=3,BC=5,则DE的长为( )