题目内容
同一条直线上有A、B、C、D四点,已知AD=
DB,AC=
CB,且CD=2cm,求AB的长.
| 5 |
| 9 |
| 9 |
| 5 |
考点:两点间的距离
专题:
分析:本题没有给出图形,在画图时,应考虑到A、B、C、D四点之间的位置关系的多种可能,再根据题意画出图形解题.
解答: 解:依题意,有以下4种情况:
解:依题意,有以下4种情况:
情况1:如图1
∵AD=
DB,AC=
CB,
∴设DB=18x,则AD=10x,CB=35x,
∵CD=DB+BC=2cm,
∴18x+35x=53x=2,
∴x=
,
∴AB=AD+DB=28x=28×
=
(cm).
情况2:如图2,
 ∵AD=
∵AD=
DB,AC=
CB,
∴设DB=18x,则AD=10x,AB=8x,CB=10x,
∵CD=DB+BC=2cm,
∴18x+10x=28x=2,
∴x=
,
∴AB=8x=
(cm).
情况3:如图3,
 ∵AD+DB=AB=AC+CB,AB=AD+DB=
∵AD+DB=AB=AC+CB,AB=AD+DB=
DB+DB,
∴DB=
AB,AD=
AB,AB=AC+CB=
CB+CB,
∴CB=
AB,AC=
AB
∴CD=AC-AD=
AB=2,AB=3.5CD=7(cm);
情况4:如图4,
 ∵BD-AD=AB=AC+BC,AB=BD-AD=BD-
∵BD-AD=AB=AC+BC,AB=BD-AD=BD-
BD,
∴BD=
AB,AD=
AB,AB=AC+CB=
CB+CB,
∴CB=
AB,AC=
AB
∴CD=AD+AC=
AB+
AB=
AB=2,AB=
(cm).
综上所述,AB的长为
cm或
cm或7cm.
 解:依题意,有以下4种情况:
解:依题意,有以下4种情况:情况1:如图1
∵AD=
| 5 |
| 9 |
| 9 |
| 5 |
∴设DB=18x,则AD=10x,CB=35x,
∵CD=DB+BC=2cm,
∴18x+35x=53x=2,
∴x=
| 2 |
| 53 |
∴AB=AD+DB=28x=28×
| 2 |
| 53 |
| 56 |
| 53 |
情况2:如图2,
 ∵AD=
∵AD=| 5 |
| 9 |
| 9 |
| 5 |
∴设DB=18x,则AD=10x,AB=8x,CB=10x,
∵CD=DB+BC=2cm,
∴18x+10x=28x=2,
∴x=
| 1 |
| 14 |
∴AB=8x=
| 4 |
| 7 |
情况3:如图3,
 ∵AD+DB=AB=AC+CB,AB=AD+DB=
∵AD+DB=AB=AC+CB,AB=AD+DB=| 5 |
| 9 |
∴DB=
| 9 |
| 14 |
| 5 |
| 14 |
| 9 |
| 5 |
∴CB=
| 5 |
| 14 |
| 9 |
| 14 |
∴CD=AC-AD=
| 2 |
| 7 |
情况4:如图4,
 ∵BD-AD=AB=AC+BC,AB=BD-AD=BD-
∵BD-AD=AB=AC+BC,AB=BD-AD=BD-| 5 |
| 9 |
∴BD=
| 9 |
| 4 |
| 5 |
| 4 |
| 9 |
| 5 |
∴CB=
| 5 |
| 14 |
| 9 |
| 14 |
∴CD=AD+AC=
| 5 |
| 4 |
| 9 |
| 14 |
| 53 |
| 28 |
| 56 |
| 53 |
综上所述,AB的长为
| 56 |
| 53 |
| 4 |
| 7 |
点评:本题考查的是两点间的距离,熟知各线段之间的和、差及倍数关系是解答此题的关键.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
某钢铁厂1月份生产某种钢材5万吨,3月份生产这种钢材7.2万吨,设平均每月增长的百分率为x,则根据题意可列方程为( )
| A、5(1+x)=7.2 |
| B、5(1+x2)=7.2 |
| C、5(1+x)2=7.2 |
| D、7.2(1+x)2=5 |
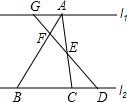 如图,l1∥l2,AF=
如图,l1∥l2,AF= 利用圆规和直尺分别作圆内接正三角形和圆内接正四边形.
利用圆规和直尺分别作圆内接正三角形和圆内接正四边形. 如图所示:点P为∠AOB内一点,分别作出P点关于OA、OB的对称点P1,P2,连接P1P2交OA于M,交OB于N,△PMN的周长为15cm,P1P2=
如图所示:点P为∠AOB内一点,分别作出P点关于OA、OB的对称点P1,P2,连接P1P2交OA于M,交OB于N,△PMN的周长为15cm,P1P2=