题目内容
 如图,在Rt△ABC中,∠BAC=90°,过顶点A的直线DE∥BC,∠ABC,∠ACB的平分线分别交DE于点E、D,若AC=3,BC=5,则DE的长为( )
如图,在Rt△ABC中,∠BAC=90°,过顶点A的直线DE∥BC,∠ABC,∠ACB的平分线分别交DE于点E、D,若AC=3,BC=5,则DE的长为( )| A、6 | B、7 | C、8 | D、9 |
考点:等腰三角形的判定与性质,平行线的性质,勾股定理
专题:
分析:在Rt△ABC中,利用勾股定理求得AB=4;然后由平行线的性质、角平分线的性质推知∠E=∠ABE,则AB=AE.同理可得AD=AC,所以线段DE的长度转化为线段AB、AC的和.
解答:解:在Rt△ABC中,∠BAC=90°,AC=3,BC=5,根据勾股定理,得AB=4,
∵DE∥BC,
∴∠E=∠EBC.
∵BE平分∠ABC,
∴∠ABE=∠EBC,
∴∠E=∠ABE,
∴AB=AE.
同理可得:AD=AC,
∴DE=AD+AE=AB+AC=7.
故选B.
∵DE∥BC,
∴∠E=∠EBC.
∵BE平分∠ABC,
∴∠ABE=∠EBC,
∴∠E=∠ABE,
∴AB=AE.
同理可得:AD=AC,
∴DE=AD+AE=AB+AC=7.
故选B.
点评:本题综合考查了勾股定理、平行线的性质以及等腰三角形的判定与性质.根据勾股定理求得AB是本题的重点.

练习册系列答案
相关题目
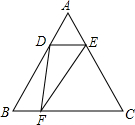 如图所示,在△ABC中,D是AB上一点,F是BC上一点,DE∥BC,交AC于点E,若△ADE与△ABC的面积的比为1:9,则△ADE与△DEF的面积的比为
如图所示,在△ABC中,D是AB上一点,F是BC上一点,DE∥BC,交AC于点E,若△ADE与△ABC的面积的比为1:9,则△ADE与△DEF的面积的比为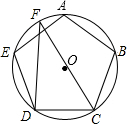 如图,正五边形ABCDE内接于圆O,F是圆O上一点,则∠CFD=
如图,正五边形ABCDE内接于圆O,F是圆O上一点,则∠CFD=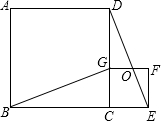 如图,四边形ABCD、CEFG都是正方形,点G在线段CD上,连接BG、DE,DE和FG相交于点O,设AB=a,CG=b(a>b).下列结论:①△BCG≌△DCE;②BG⊥DE;③
如图,四边形ABCD、CEFG都是正方形,点G在线段CD上,连接BG、DE,DE和FG相交于点O,设AB=a,CG=b(a>b).下列结论:①△BCG≌△DCE;②BG⊥DE;③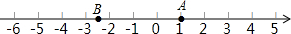 根据下面给出的数轴,解答下面的问题:
根据下面给出的数轴,解答下面的问题: 如图,l1∥l2,AF=
如图,l1∥l2,AF= 如图,弦CD垂直于⊙O的直径AB,垂足为H,CD=6,BD=
如图,弦CD垂直于⊙O的直径AB,垂足为H,CD=6,BD=