题目内容
已知函数y=x2-4x+3,该函数图象与x轴有 个交点,请作图予以验证.
考点:抛物线与x轴的交点
专题:计算题
分析:计算判别式的值得到△>0,根据△=b2-4ac决定抛物线与x轴的交点个数可判断抛物线与x轴有2个交点,然后把抛物线解析式配成顶点式,利用描点法画出抛物线,由图象可得抛物线与x轴有2个交点.
解答:解:∵△=(-4)2-4×1×3>0,
∴函数y=x2-4x+3的图象与x轴有2个交点.
y=x2-4x+3=(x-2)2,-1,抛物线的对称轴为直线x=2,顶点坐标为(2,-1),
如图:
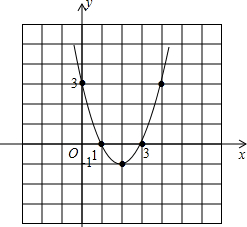
故答案为2.
∴函数y=x2-4x+3的图象与x轴有2个交点.
y=x2-4x+3=(x-2)2,-1,抛物线的对称轴为直线x=2,顶点坐标为(2,-1),
如图:

故答案为2.
点评:本题考查了抛物线与x轴的交点:二次函数y=ax2+bx+c(a,b,c是常数,a≠0)的交点与一元二次方程ax2+bx+c=0根之间的关系,△=b2-4ac决定抛物线与x轴的交点个数:△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
 如图所示:点P为∠AOB内一点,分别作出P点关于OA、OB的对称点P1,P2,连接P1P2交OA于M,交OB于N,△PMN的周长为15cm,P1P2=
如图所示:点P为∠AOB内一点,分别作出P点关于OA、OB的对称点P1,P2,连接P1P2交OA于M,交OB于N,△PMN的周长为15cm,P1P2= 如图,弦CD垂直于⊙O的直径AB,垂足为H,CD=6,BD=
如图,弦CD垂直于⊙O的直径AB,垂足为H,CD=6,BD=
 如图所示,已知点A、F、E、C在同一直线上,AB∥CD,∠ABE=∠CDF,AF=CE.
如图所示,已知点A、F、E、C在同一直线上,AB∥CD,∠ABE=∠CDF,AF=CE. 如图,∠BOD的度数是
如图,∠BOD的度数是