题目内容
4．
如图，在Rt△ABC中，∠ACB=90°，DE过点C，且DE∥AB，若∠ACD=55°，则∠B的度数是35°．
分析 根据“∠ACB=90°和∠ACD=55°”先求出∠BCE的度数，再根据两直线平行，内错角相等即可求出∠B．
解答 解：∵∠ACB=90°，∠ACD=55°，
∴∠BCE=180°-90°-55°=35°，
∵DE∥AB，
∴∠B=∠BCE=35°．
故答案为：35°．
点评 本题考查的是的是平行线的性质，用到的知识点为：两直线平行，内错角相等．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
14．下列根式中，是最简二次根式的是（ ）
| A． | $\sqrt{0.3}$ | B． | $\sqrt{\frac{2}{5}}$ | C． | $\sqrt{2a{b}^{2}c}$ | D． | $\sqrt{{a}^{2}+9}$ |
15．下列多项式中，能用公式法分解因式的是（ ）
| A． | -m2+n2 | B． | a2-2ab-b2 | C． | m2+n2 | D． | -a2-b2 |
12．
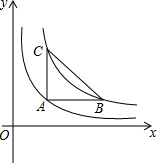已知b＞a＞0，如图，过函数y=$\frac{a}{x}$（x＞0）图象上一点A作AB平行于x轴，交函数y=$\frac{b}{x}$（x＞0）的图象于点B，过点A作AC平行于y轴，交函数y=$\frac{b}{x}$（x＞0）的图象于点C，则△ABC的面积为（ ）
已知b＞a＞0，如图，过函数y=$\frac{a}{x}$（x＞0）图象上一点A作AB平行于x轴，交函数y=$\frac{b}{x}$（x＞0）的图象于点B，过点A作AC平行于y轴，交函数y=$\frac{b}{x}$（x＞0）的图象于点C，则△ABC的面积为（ ）| A． | $\frac{a-b}{2}$ | B． | $\frac{（a-b）^{2}}{2}$ | C． | $\frac{（a-b）^{2}}{2a}$ | D． | $\frac{（a-b）^{2}}{2b}$ |
如图，在四边形ABCD中，AB=AD，BC=DC，E为AC上的一动点（不与A重合），求证：BE=DE．
16．不等式组$\left\{\begin{array}{l}{x＜-2}\\{x＞-3}\end{array}\right.$的解集是（ ）
| A． | x＜-3 | B． | x＜-2 | C． | -3＜x＜-2 | D． | 无解 |
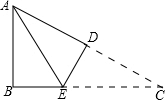如图，在△ABC中，AB=3cm，BC=7cm，将△ABC折叠，使点C与点A重合，折痕为DE，则△ABE的周长为10cm．