题目内容
9. 如图,在四边形ABCD中,AB=AD,BC=DC,E为AC上的一动点(不与A重合),求证:BE=DE.
如图,在四边形ABCD中,AB=AD,BC=DC,E为AC上的一动点(不与A重合),求证:BE=DE.
分析 要证BE=DE,先证△ADC≌△ABC,再证△ADE≌△ABE即可.
解答 解:在△ABC和△ADC中,
$\left\{\begin{array}{l}{AB=AD}\\{AC=AC}\\{BC=DC}\end{array}\right.$,
∴△ABC≌△ADC(SSS),
∴∠DAE=∠BAE,
在△ADE和△ABE中,
$\left\{\begin{array}{l}{AB=AD}\\{∠DAE=∠BAE}\\{AE=AE}\end{array}\right.$,
∴△ADE≌△ABE(SAS),
∴BE=DE.
点评 本题重点考查了三角形全等的判定定理,利用全等得出结论证明三角形全等是常用的方法.

练习册系列答案
相关题目
1. 如图,在?ABCD中,对角线AC、BD相交于点O,AC=10,BD=6,AD=4,则?ABCD的面积是( )
如图,在?ABCD中,对角线AC、BD相交于点O,AC=10,BD=6,AD=4,则?ABCD的面积是( )
 如图,在?ABCD中,对角线AC、BD相交于点O,AC=10,BD=6,AD=4,则?ABCD的面积是( )
如图,在?ABCD中,对角线AC、BD相交于点O,AC=10,BD=6,AD=4,则?ABCD的面积是( )| A. | 12 | B. | 12$\sqrt{3}$ | C. | 24 | D. | 30 |
18.弹簧挂上适当的重物后会按一定的规律伸长,已知一弹簧的长度y(cm)与所挂物体的质量x(kg)之间的关系如表:
(1)如表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)写出y与x之间的关系式;
(3)当所挂物体的质量为11.5kg时,求弹簧的长度.
| 所挂物体的质量x(kg) | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 弹簧的长度y(cm) | 15 | 15.6 | 16.2 | 16.8 | 17.4 | 18 | 18.6 |
(2)写出y与x之间的关系式;
(3)当所挂物体的质量为11.5kg时,求弹簧的长度.
 如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上,已知纸板的两条直角边DE=50cm,EF=25cm,测得边DF离地面的高度AC=1.6m,CD=10m,则树高AB=6.6m.
如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上,已知纸板的两条直角边DE=50cm,EF=25cm,测得边DF离地面的高度AC=1.6m,CD=10m,则树高AB=6.6m.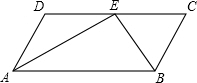 如图,平行四边形ABCD中,点E是DC边上一点,连接AE、BE,已知AE是∠DAB的平分线,BE是∠CBA的平分线.
如图,平行四边形ABCD中,点E是DC边上一点,连接AE、BE,已知AE是∠DAB的平分线,BE是∠CBA的平分线. 如图,在Rt△ABC中,∠ACB=90°,DE过点C,且DE∥AB,若∠ACD=55°,则∠B的度数是35°.
如图,在Rt△ABC中,∠ACB=90°,DE过点C,且DE∥AB,若∠ACD=55°,则∠B的度数是35°. 已知在△ABC中,AC=8,∠A=30°,∠B=45°,求AB和BC的长.
已知在△ABC中,AC=8,∠A=30°,∠B=45°,求AB和BC的长.