题目内容
14.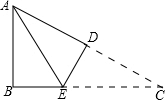 如图,在△ABC中,AB=3cm,BC=7cm,将△ABC折叠,使点C与点A重合,折痕为DE,则△ABE的周长为10cm.
如图,在△ABC中,AB=3cm,BC=7cm,将△ABC折叠,使点C与点A重合,折痕为DE,则△ABE的周长为10cm.
分析 首先根据翻折变换的性质,可得AE=CE,然后根据三角形的周长的求法,可得△ABE的周长等于AB和BC的长度和,据此解答即可.
解答 解:∵将△ABC折叠,使点C与点A重合,折痕为DE,
∴AE=CE,
∴△ABE的周长=AB+BE+AE
=AB+(BE+CE)
=AB+BC
=3+7
=10(cm),
即△ABE的周长为10cm.
故答案为:10cm.
点评 (1)此题主要考查了翻折变换(折叠问题),要熟练掌握,解答此题的关键是要明确:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.
(2)此题还考查了三角形的周长的求法,要熟练掌握,解答此题的关键是判断出:BE+CE=BC.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5.一次函数y=2x-4的图象与两坐标轴交点的距离是( )
| A. | 4$\sqrt{2}$ | B. | 2$\sqrt{5}$ | C. | 2$\sqrt{6}$ | D. | 2$\sqrt{7}$ |
9. 如图,该图形绕点O按下列角度旋转后,能与原图形重合的是( )
如图,该图形绕点O按下列角度旋转后,能与原图形重合的是( )
 如图,该图形绕点O按下列角度旋转后,能与原图形重合的是( )
如图,该图形绕点O按下列角度旋转后,能与原图形重合的是( )| A. | 45° | B. | 60° | C. | 90° | D. | 120° |
6.正比例函数y=-3x的大致图象是( )
| A. |  | B. |  | C. |  | D. |  |
3.实验中学为了了解该校学生课外阅读情况,随机抽查了50名学生,统计他们平均每周课外阅读时间t(h).枨据时间t的长短分为A,B,C,D四类.下面是根据所抽杳的人数绘制了不完整的统计表.其中a、b、c和d是满足a<b<c<d的正整数,请解答下面的问题:
50名学生平均每天课外阅读时间统计表
(1)写出表格中a+b+c+d的值.并求表格中的a、b、c、d的值;
(2)如果每分钟阅读200个字,每天坚持课外阅读时间为0.5h,一年(365天)能阅读多少本(10万字/本)书籍?
50名学生平均每天课外阅读时间统计表
| 类别 | A | B | C | D |
| 时间t(h) | t<1 | 1≤t<2 | 2≤t<3 | t≥3 |
| 人数 | 5a | 5b | 5c | 5d |
(2)如果每分钟阅读200个字,每天坚持课外阅读时间为0.5h,一年(365天)能阅读多少本(10万字/本)书籍?
 如图,在Rt△ABC中,∠ACB=90°,DE过点C,且DE∥AB,若∠ACD=55°,则∠B的度数是35°.
如图,在Rt△ABC中,∠ACB=90°,DE过点C,且DE∥AB,若∠ACD=55°,则∠B的度数是35°. 如图,菱形ABCD的对角线AC上有一动点P,BC=6,∠ABC=150°,则线段AP+BP+PD的最小值为6$\sqrt{2}$.
如图,菱形ABCD的对角线AC上有一动点P,BC=6,∠ABC=150°,则线段AP+BP+PD的最小值为6$\sqrt{2}$.