题目内容
19．
如图，在四边形ABCD中，∠1=∠2，∠3=∠4，且∠D+∠C=220°，求∠AOB的度数．
分析 首先根据四边形内角和为360度计算出∠DAB+∠ABC=360°-220°=140°，再根据∠1=∠2，∠3=∠4计算出∠2+∠3=70°，然后利用三角形内角和为180度计算出∠AOB的度数．
解答 解：∵∠D+∠C+∠DAB+∠ABC=360°，∠D+∠C=220°，
∴∠DAB+∠ABC=360°-220°=140°，
∵∠1=∠2，∠3=∠4，
∴∠2+∠3=70°，
∴∠AOB=180°-70°=110°．
点评 此题主要考查了多边形的内角，关键是掌握四边形内角和为360°，三角形内角和为180°．
练习册系列答案
相关题目
如图，在△ABC中，AD是高，AE是角平分线，∠B=20°，∠C=60°．求∠EAD的度数．
7．
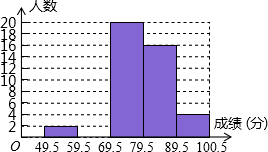某班数学课代表小华对本班上学期期末考试数学成绩作了统计分析，绘制成如下频数、频率统计表和频数分布直方图，请你根据图表提供的信息，解答下列问题：
根据上述信息，完成下列问题：
（1）频数、频率统计表中，a=8；b=0.08；
（2）请将频数分布直方图补充完整；
（3）若成绩在79.5分以上为优秀，则该班优秀人数是多少？
某班数学课代表小华对本班上学期期末考试数学成绩作了统计分析，绘制成如下频数、频率统计表和频数分布直方图，请你根据图表提供的信息，解答下列问题：| 分组 | 49.5～59.5 | 59.5～69.5 | 69.5～79.5 | 79.5～89.5 | 89.5～100.5 | 合计 |
| 频数 | 2 | a | 20 | 16 | 4 | 50 |
| 频率 | 0.04 | 0.16 | 0.40 | 0.32 | b | 1 |
（1）频数、频率统计表中，a=8；b=0.08；
（2）请将频数分布直方图补充完整；
（3）若成绩在79.5分以上为优秀，则该班优秀人数是多少？
4．下列由左到右的变形，是因式分解的是（ ）
| A． | （a+6）（a-6）=a2-36 | B． | x2-8x+16=（x-4）2 | ||
| C． | a2-b2+1=（a+b）（a-b）+1 | D． | （x-2）（x+3）=（x+3）（x-2） |
11．下列抛物线，对称轴是直线x=0.5的是（ ）
| A． | y=$\frac{1}{2}$x2 | B． | y=（x+0.5）2+2 | C． | y=（x-0.5）2+2 | D． | y=x2-2x-0.5 |
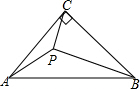如图，在△ABC中，∠ACB=90°，AC=BC，P为三角形内部一点，且PC=3，PA=5，PB=7，则△PAB的面积为14．