题目内容
18.在△ABC中,若AC=BC,∠ACB=90°,AB=10,则AC=5$\sqrt{2}$.分析 根据勾股定理列出方程即可解决问题.
解答 解:∵在△ABC中,若AC=BC,∠ACB=90°,AB=10,
∴AC2+BC2=AB2,即2AC2=100,
∴AC=5$\sqrt{2}$.
故答案为5$\sqrt{2}$.
点评 本题考查等腰直角三角形的性质、勾股定理等知识,熟练掌握勾股定理是解决问题的关键.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
6.若方程组$\left\{\begin{array}{l}{2x+y=5}\\{x+2y=a-3}\end{array}\right.$的解满足x+y的值为非负数,则a满足( )
| A. | a<-2 | B. | a≤-2 | C. | a≤2 | D. | a≥-2 |
13.在:0,-2,1,$\frac{1}{2}$这四个数中,绝对值最小的数是 ( )
| A. | 0 | B. | -2 | C. | 1 | D. | $\frac{1}{2}$ |
10.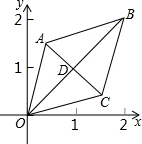 如图,已知菱形OABC的两个顶点O(0,0),B(2,2),若将菱形绕点O以每秒45°的速度逆时针旋转,则第2017秒时,菱形两对角线交点D的纵坐标为( )
如图,已知菱形OABC的两个顶点O(0,0),B(2,2),若将菱形绕点O以每秒45°的速度逆时针旋转,则第2017秒时,菱形两对角线交点D的纵坐标为( )
 如图,已知菱形OABC的两个顶点O(0,0),B(2,2),若将菱形绕点O以每秒45°的速度逆时针旋转,则第2017秒时,菱形两对角线交点D的纵坐标为( )
如图,已知菱形OABC的两个顶点O(0,0),B(2,2),若将菱形绕点O以每秒45°的速度逆时针旋转,则第2017秒时,菱形两对角线交点D的纵坐标为( )| A. | -1 | B. | 1 | C. | -$\sqrt{2}$ | D. | $\sqrt{2}$ |
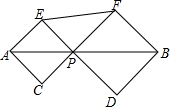 如图,AB=4,P在线段AB上,以.AP,BP为对角线,作正方形AEPC与正方形BFPD,则EF的最小值为2.
如图,AB=4,P在线段AB上,以.AP,BP为对角线,作正方形AEPC与正方形BFPD,则EF的最小值为2.



 如图,已知OD⊥AB,OE⊥OC,则图中互余的角有与4对.
如图,已知OD⊥AB,OE⊥OC,则图中互余的角有与4对.