题目内容
 如图,AB是⊙O的直径,点C在⊙O上,过点C作⊙O的切线CM.
如图,AB是⊙O的直径,点C在⊙O上,过点C作⊙O的切线CM.(1)求证:∠ACM=∠ABC;
(2)延长BC到D,使BC=CD,连接AD与CM交于点E,若⊙O的半径为3,ED=2,求△ACE的外接圆的半径.
考点:切线的性质,勾股定理,圆周角定理,相似三角形的判定与性质
专题:几何综合题
分析:(1)连接OC,由∠ABC+∠BAC=90°及CM是⊙O的切线得出∠ACM+∠ACO=90°,再利用∠BAC=∠ACO,得出结论,
(2)连接OC,得出△AEC是直角三角形,△AEC的外接圆的直径是AC,利用△ABC∽△CDE,求出AC,
(2)连接OC,得出△AEC是直角三角形,△AEC的外接圆的直径是AC,利用△ABC∽△CDE,求出AC,
解答:(1)证明:如图,连接OC,

∵AB为⊙O的直径,
∴∠ACB=90°,
∴∠ABC+∠BAC=90°,
又∵CM是⊙O的切线,
∴OC⊥CM,
∴∠ACM+∠ACO=90°,
∵CO=AO,
∴∠BAC=∠ACO,
∴∠ACM=∠ABC;
(2)解:∵BC=CD,∠ACB=90°,
∴∠OAC=∠CAD,
∵OA=OC,
∴∠OAC=∠OCA,
∴∠OCA=∠CAD,
∴OC∥AD,
又∵OC⊥CE,
∴AD⊥CE,
∴△AEC是直角三角形,
∴△AEC的外接圆的直径是AC,
又∵∠ABC+∠BAC=90°,∠ACM+∠ECD=90°,
∴△ABC∽△CDE,
∴
=
,
⊙O的半径为3,
∴AB=6,
∴
=
,
∴BC2=12,
∴BC=2
,
∴AC=
=2
,
∴△AEC的外接圆的半径为
.

∵AB为⊙O的直径,
∴∠ACB=90°,
∴∠ABC+∠BAC=90°,
又∵CM是⊙O的切线,
∴OC⊥CM,
∴∠ACM+∠ACO=90°,
∵CO=AO,
∴∠BAC=∠ACO,
∴∠ACM=∠ABC;
(2)解:∵BC=CD,∠ACB=90°,
∴∠OAC=∠CAD,
∵OA=OC,
∴∠OAC=∠OCA,
∴∠OCA=∠CAD,
∴OC∥AD,
又∵OC⊥CE,
∴AD⊥CE,
∴△AEC是直角三角形,
∴△AEC的外接圆的直径是AC,
又∵∠ABC+∠BAC=90°,∠ACM+∠ECD=90°,
∴△ABC∽△CDE,
∴
| AB |
| CD |
| BC |
| ED |
⊙O的半径为3,
∴AB=6,
∴
| 6 |
| CD |
| BC |
| 2 |
∴BC2=12,
∴BC=2
| 3 |
∴AC=
| 36-12 |
| 6 |
∴△AEC的外接圆的半径为
| 6 |
点评:本题考查了切线的性质:圆的切线垂直于经过切点的半径.也考查了勾股定理、圆周角定理和相似三角形的判定与性质.解题的关键是找准角的关系.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
 如图,∠1=∠2,∠DAB=∠BCD.下列四个结论中,错误的是( )
如图,∠1=∠2,∠DAB=∠BCD.下列四个结论中,错误的是( )| A、AB∥CD |
| B、AD∥BC |
| C、∠B=∠D |
| D、∠DCA=∠DAC |
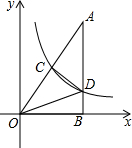 如图,Rt△AOB的一条直角边OB在x轴上,双曲线y=
如图,Rt△AOB的一条直角边OB在x轴上,双曲线y= 如图,已知抛物线y=ax2+bx+c与x轴的一个交点为A(3,0),与y轴的交点为B(0,3),其顶点为C,对称轴为x=1.
如图,已知抛物线y=ax2+bx+c与x轴的一个交点为A(3,0),与y轴的交点为B(0,3),其顶点为C,对称轴为x=1. 如图,在菱形ABCD中,对角线AC、BD相交于点O,过点O作一条直线分别交DA、BC的延长线于点E、F,连接BE、DF.
如图,在菱形ABCD中,对角线AC、BD相交于点O,过点O作一条直线分别交DA、BC的延长线于点E、F,连接BE、DF. 如图,将透明三角形纸片PAB的直角顶点P落在第四象限,顶点A、B分别落在反比例函数y=
如图,将透明三角形纸片PAB的直角顶点P落在第四象限,顶点A、B分别落在反比例函数y=