题目内容
 如图,在菱形ABCD中,对角线AC、BD相交于点O,过点O作一条直线分别交DA、BC的延长线于点E、F,连接BE、DF.
如图,在菱形ABCD中,对角线AC、BD相交于点O,过点O作一条直线分别交DA、BC的延长线于点E、F,连接BE、DF.(1)求证:四边形BFDE是平行四边形;
(2)若EF⊥AB,垂足为M,tan∠MBO=
| 1 |
| 2 |
考点:菱形的性质,平行四边形的判定
专题:几何综合题
分析:(1)根据两直线平行,内错角相等可得∠AEO=∠CFO,然后利用“角角边”证明△AEO和△CFO全等,根据全等三角形对应边相等可得OE=OF,再根据对角线互相平分的四边形是平行四边形证明即可;
(2)设OM=x,根据∠MBO的正切值表示出BM,再根据△AOM和△OBM相似,利用相似三角形对应边成比例求出AM,然后根据△AEM和△BFM相似,利用相似三角形对应边成比例求解即可.
(2)设OM=x,根据∠MBO的正切值表示出BM,再根据△AOM和△OBM相似,利用相似三角形对应边成比例求出AM,然后根据△AEM和△BFM相似,利用相似三角形对应边成比例求解即可.
解答:(1)证明:在菱形ABCD中,AD∥BC,OA=OC,OB=OD,
∴∠AEO=∠CFO,
在△AEO和△CFO中,
,
∴△AEO≌△CFO(AAS),
∴OE=OF,
又∵OB=OD,
∴四边形BFDE是平行四边形;
(2)解:设OM=x,
∵EF⊥AB,tan∠MBO=
,
∴BM=2x,
又∵AC⊥BD,
∴∠AOM=∠OBM,
∴△AOM∽△OBM,
∴
=
,
∴AM=
=
x,
∵AD∥BC,
∴△AEM∽△BFM,
∴EM:FM=AM:BM=
x:2x=1:4.

∴∠AEO=∠CFO,
在△AEO和△CFO中,
|
∴△AEO≌△CFO(AAS),
∴OE=OF,
又∵OB=OD,
∴四边形BFDE是平行四边形;
(2)解:设OM=x,
∵EF⊥AB,tan∠MBO=
| 1 |
| 2 |
∴BM=2x,
又∵AC⊥BD,
∴∠AOM=∠OBM,
∴△AOM∽△OBM,
∴
| AM |
| OM |
| OM |
| BM |
∴AM=
| OM2 |
| BM |
| 1 |
| 2 |
∵AD∥BC,
∴△AEM∽△BFM,
∴EM:FM=AM:BM=
| 1 |
| 2 |
点评:本题考查了菱形的性质,全等三角形的判定与性质,相似三角形的判定与性质,锐角三角函数的定义,难点在于(2)两次求出三角形相似.

练习册系列答案
相关题目
 如图,在Rt△ABC中,∠ACB=90°,以AC为直径作⊙O交AB于点D点,连接CD.
如图,在Rt△ABC中,∠ACB=90°,以AC为直径作⊙O交AB于点D点,连接CD. 如图,AB是⊙O的直径,点C在⊙O上,过点C作⊙O的切线CM.
如图,AB是⊙O的直径,点C在⊙O上,过点C作⊙O的切线CM.
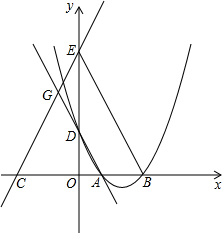 已知抛物线y=x2-(k+2)x+
已知抛物线y=x2-(k+2)x+