题目内容
13. 已知AB为⊙0的直径,DE为⊙0的弦,连DA,EB.
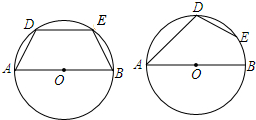
已知AB为⊙0的直径,DE为⊙0的弦,连DA,EB.(1)如图1,若∠A=∠B=60°,求证:AD=DE=BE.
(2)如图2.若∠A+∠B=120°,试探究DE与AB的数量关系.
分析 (1)连接OD,OE,则OA=OD=OE=OB,得出△AOD,△DOE,△BOE都是全等的正三角形,从而证得结论;
(2)连接OD,OE,设∠A=x,则∠B=120°-x,∠E=180°-x,根据等腰三角形的性质得出∠OEB=∠OBE=120°-x,根据圆内接四边形的性质求得∠OED=180°-x-(120°-x)=60°,从而求得△ODE是等边三角形,即可得出DE=$\frac{1}{2}$AB.
解答 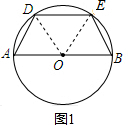 解:(1)如图1,连接OD,OE,则OA=OD=OE=OB,
解:(1)如图1,连接OD,OE,则OA=OD=OE=OB,
∵∠A=∠B=60°,
∴△AOD,△DOE,△BOE都是全等的正三角形,
∴AD=DE=BE;
(2)连接OD,OE,
设∠A=x,则∠B=120°-x,∠E=180°-x,
∵OB=OE,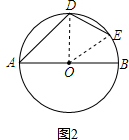
∴∠OEB=∠OBE=120°-x,
∴∠OED=180°-x-(120°-x)=60°,
又∵OE=OD,
∴△ODE是等边三角形,
∴DE=OD=OE,
∴DE=$\frac{1}{2}$AB.
点评 本题考查了圆心角、弧、弦的关系,等边三角形的判定和性质,作出辅助线,证得等边三角形是解题的关键.

练习册系列答案
相关题目
4.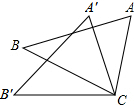 如图,△ACB≌△A′CB,点A和点A′,点B和点B′是对应点,∠BCB′=30°,则∠ACA′的度数为( )
如图,△ACB≌△A′CB,点A和点A′,点B和点B′是对应点,∠BCB′=30°,则∠ACA′的度数为( )
 如图,△ACB≌△A′CB,点A和点A′,点B和点B′是对应点,∠BCB′=30°,则∠ACA′的度数为( )
如图,△ACB≌△A′CB,点A和点A′,点B和点B′是对应点,∠BCB′=30°,则∠ACA′的度数为( )| A. | 20° | B. | 30° | C. | 35° | D. | 40° |
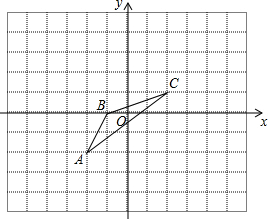 如图,在平面直角坐标系中,
如图,在平面直角坐标系中, 如图,等边△ABC内接于⊙O,AD是直径,则∠CBD=30°.
如图,等边△ABC内接于⊙O,AD是直径,则∠CBD=30°.