题目内容
2. 如图,等边△ABC内接于⊙O,AD是直径,则∠CBD=30°.
如图,等边△ABC内接于⊙O,AD是直径,则∠CBD=30°.
分析 根据等边三角形性质求出∠ABC=∠C=60°,根据圆周角定理求出∠D=∠C=60°,∠ABD=90°,即可求出答案.
解答 解:∵△ABC是等边三角形,
∴∠ABC=∠C=60°,
根据圆周角定理得:∠D=∠C=60°,
∵AD为直径,
∴∠ABD=90°,
∴∠CBD=90°-60°=30°,
故答案为:30.
点评 本题考查了圆周角定理和等边三角形的性质的应用,能求出∠ABD和∠ABC的度数是解此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.方程$\frac{x}{1×3}$+$\frac{x}{3×5}$+…+$\frac{x}{2013×2015}$=2014的解是( )
| A. | 2014 | B. | 2015 | C. | 4028 | D. | 4030 |
17.下列各数-4、+3、-2、0、-1、a-M(M是有理数),其中一定是负数的有( )个.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
14. 如图,⊙O的内接四边形ABCD两组对边的延长线分别交于点E,F,∠E=α,∠F=β,则∠A=( )
如图,⊙O的内接四边形ABCD两组对边的延长线分别交于点E,F,∠E=α,∠F=β,则∠A=( )
 如图,⊙O的内接四边形ABCD两组对边的延长线分别交于点E,F,∠E=α,∠F=β,则∠A=( )
如图,⊙O的内接四边形ABCD两组对边的延长线分别交于点E,F,∠E=α,∠F=β,则∠A=( )| A. | α+β | B. | $\frac{α+β}{2}$ | C. | 180-α-β | D. | $\frac{180-α-β}{2}$ |
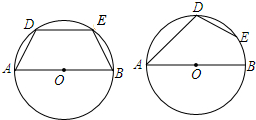 已知AB为⊙0的直径,DE为⊙0的弦,连DA,EB.
已知AB为⊙0的直径,DE为⊙0的弦,连DA,EB. 如图,互相垂直的两条公路AM、AN旁有一矩形花园ABCD,其中AB=30米,AD=20米.现欲将其扩建成一个三角形花园APQ,要求P在射线AM上,Q在射线AN上,且PQ经过点C.
如图,互相垂直的两条公路AM、AN旁有一矩形花园ABCD,其中AB=30米,AD=20米.现欲将其扩建成一个三角形花园APQ,要求P在射线AM上,Q在射线AN上,且PQ经过点C. 已知m≥2,n≥2,且m,n均为正整数,如果将具有mn形式的有理数进行如图方式的“分解”,那么请把43分解的结果填入右图的方框内.
已知m≥2,n≥2,且m,n均为正整数,如果将具有mn形式的有理数进行如图方式的“分解”,那么请把43分解的结果填入右图的方框内.