Question

14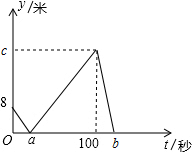．甲、乙两人在直线跑道上同起点、同终点、同方向匀速跑步500米，先到终点的人在原地休息．已知甲先出发2秒．在跑步过程中，甲、乙两人间的距离y（米）与乙出发的时间t（秒）之间的关系如图所示，下列结论中正确的有几个？（　　）
（1）甲速为每秒4米；
（2）乙速为每秒5米；
（3）a=8；
（4）b=100；
（5）c=125．

• A． 4个
• B． 2个
• C． 3个
• D． 1个

Answer 1

分析 （1）由图得：乙开始跑时，距离甲8米，即甲2秒跑了8米，计算出甲速为每秒4米；
（2）两人的速度不同，乙比甲快，发现100米时两人距离最远，这时是乙到达终点的时间，由此可以计算乙的速度为每秒5米；
（3）a是两人相遇的时间，相遇时两人的路程相等，列方程可以得出；
（4）b是甲到达终点的时间，因为此图中的t是乙的时间，所以要减去2秒；
（5）c是100秒时，两人的距离．

解答 解：（1）8÷2=4，所以甲速为每秒4米，故此结论正确；
（2）500÷100=5，所以乙速为每秒5米，故此结论正确；
（3）由图可知，两人a小时相遇，
则5a=4（a+2），
a=8，
故此结论正确；
（4）由图可知：乙100秒到终点，
而甲需要的时间为：500÷4=125秒，所以b=125-2=123，故此结论不正确；
（5）当乙100秒到终点时，甲、乙二人的距离为：100×5-4（100+2）=92米，
所以c=92，故此结论不正确；
所以本题结论中正确的有3个，故选C．

点评 本题是一次函数的应用，属于行程问题，考查了由图得出已知信息，再解决问题；要明确时间、路程、速度的关系，本题有两个人，速度不同，但同起点、同终点、同方向匀速跑步500米，理解这一句话是关键，利用数形结合解决问题．