题目内容
9.平面直角坐标系中,直线y=-$\frac{1}{2}$x+2和x、y轴交于A、B两点,在第二象限内找一点P,使△PBO和△AOB相似的三角形个数为( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 根据相似三角形的相似条件,画出图形即可解决问题.
解答 解:如图,
①分别过点O、点A作AB、OB的平行线交于点P1,则△OAP1与△AOB相似(全等),
②作AP2⊥OP1,垂足为P2则△AOP2与△AOB相似.
③作∠AOP3=∠ABO交AP1于P3,则△AOP3与△AOB相似.
④作AP4⊥OP3垂足为P4,则△AOP4与△AOB相似.
故选C.
点评 本题考查相似三角形的判定、平行线的性质等知识,解题的关键是灵活掌握相似三角形的判定方法,属于中考常考题型.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
 (2)
(2) 
 如图,下列A,B,C,D四个三角形中,能和模板中的△ABC完全重合的是( )
如图,下列A,B,C,D四个三角形中,能和模板中的△ABC完全重合的是( )



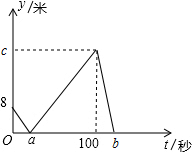 甲、乙两人在直线跑道上同起点、同终点、同方向匀速跑步500米,先到终点的人在原地休息.已知甲先出发2秒.在跑步过程中,甲、乙两人间的距离y(米)与乙出发的时间t(秒)之间的关系如图所示,下列结论中正确的有几个?( )
甲、乙两人在直线跑道上同起点、同终点、同方向匀速跑步500米,先到终点的人在原地休息.已知甲先出发2秒.在跑步过程中,甲、乙两人间的距离y(米)与乙出发的时间t(秒)之间的关系如图所示,下列结论中正确的有几个?( )