题目内容
4.已知a、b、c是△ABC的三边长,且关于x的方程(a+c)x2+2bx+a-c=0有两个相等的实数根,则△ABC的形状是等边三角形.分析 由a、b、c是△ABC的三边长,可得出a+c≠0,再由方程(a+c)x2+2bx+a-c=0有两个相等的实数根利用根的判别式△=0,即可找出a2=b2+c2,根据勾股定理的逆运用即可得出结论.
解答 解:∵a、b、c是△ABC的三边长,
∴a+c≠0.
∵方程(a+c)x2+2bx+a-c=0有两个相等的实数根,
∴△=(2b)2-4(a+c)(a-c)=4(b2+c2-a2)=0,
∴a2=b2+c2,
∴△ABC为等边三角形.
故答案为:等边三角形.
点评 本题考查了根的判别式,熟练掌握“当△=0时,方程有两个相等的两个实数根.”是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.-2016的绝对值( )
| A. | 2016 | B. | -2016 | C. | ±2016 | D. | 0 |
12.下列各式中,正确的是( )
| A. | 2<$\sqrt{15}$<3 | B. | 3<$\sqrt{15}$<4 | C. | 4<$\sqrt{15}$<5 | D. | 14<$\sqrt{15}$<16 |
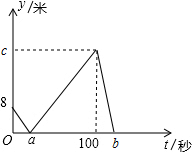 甲、乙两人在直线跑道上同起点、同终点、同方向匀速跑步500米,先到终点的人在原地休息.已知甲先出发2秒.在跑步过程中,甲、乙两人间的距离y(米)与乙出发的时间t(秒)之间的关系如图所示,下列结论中正确的有几个?( )
甲、乙两人在直线跑道上同起点、同终点、同方向匀速跑步500米,先到终点的人在原地休息.已知甲先出发2秒.在跑步过程中,甲、乙两人间的距离y(米)与乙出发的时间t(秒)之间的关系如图所示,下列结论中正确的有几个?( )
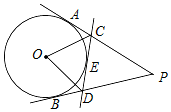 如图,PA、PB、CD是⊙O的切线,A、B、E是切点,CD分别交PA、PB于C、D两点.如∠APB=40°,则∠COD的度数为70°.
如图,PA、PB、CD是⊙O的切线,A、B、E是切点,CD分别交PA、PB于C、D两点.如∠APB=40°,则∠COD的度数为70°. 如图,△ABC为等边三角形,BD平分∠ABC,DE∥BC.
如图,△ABC为等边三角形,BD平分∠ABC,DE∥BC.