题目内容
5. 如图,已知线段AB和CD的公共部分BD=$\frac{1}{4}$CD=$\frac{1}{5}$AB,点E,F分别是AB,CD的中点,且EF=14,求AB,CD的长.
如图,已知线段AB和CD的公共部分BD=$\frac{1}{4}$CD=$\frac{1}{5}$AB,点E,F分别是AB,CD的中点,且EF=14,求AB,CD的长.
分析 先BD=x,则CD=4x,AB=5x,再根据点E,F分别是AB,CD的中点,得到EF=ED+DF=3.5x,根据EF=14,可得x的值,进而得到AB,CD的长.
解答 解:设BD=x,则CD=4x,AB=5x,
∵点E,F分别是AB,CD的中点,
∴EB=$\frac{1}{2}$AB=2.5x,DF=$\frac{1}{2}$CD=2x,
∴ED=1.5x,
∴EF=ED+DF=3.5x,
又∵EF=14,
∴3.5x=14,
解得x=4,
∴CD=4x=16cm,AB=5x=20cm.
点评 本题主要考查了两点间的距离,解决问题的关键是依据中点的定义,利用线段的和差关系进行计算.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
15.下列说法正确的个数是( )
①一组数据的众数只有一个②样本的方差越小,波动性越小,说明样本稳定性越好③一组数据的中位数一定是这组数据中的某一数据④数据:1,1,3,1,1,2的众数为4 ⑤一组数据的方差一定是正数.
①一组数据的众数只有一个②样本的方差越小,波动性越小,说明样本稳定性越好③一组数据的中位数一定是这组数据中的某一数据④数据:1,1,3,1,1,2的众数为4 ⑤一组数据的方差一定是正数.
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 4个 |
15.以下问题,不适合用全面调查的是( )
| A. | 旅客上飞机前的安检 | B. | 学校招聘教师,对应聘人员的面试 | ||
| C. | 了解全校学生的课外读书时间 | D. | 了解全国中学生的用眼卫生情况 |
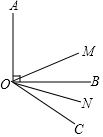 如图,已知∠AOB=90°,∠BOC=30°,OM平分∠AOC,ON平分∠BOC.
如图,已知∠AOB=90°,∠BOC=30°,OM平分∠AOC,ON平分∠BOC.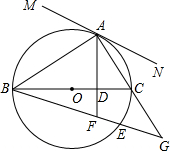 如图,BC是⊙O的直径,点A在⊙O上,AD⊥BC,垂足为D,$\underset{\widehat{AB}}{\;}$=$\widehat{AE}$,BE分别交AD、AC延长线于点F、G.
如图,BC是⊙O的直径,点A在⊙O上,AD⊥BC,垂足为D,$\underset{\widehat{AB}}{\;}$=$\widehat{AE}$,BE分别交AD、AC延长线于点F、G.