题目内容
13.一个封闭的纸箱中有不同颜色的球100个,小敏将球搅匀后,从中随机摸出一个球记下其颜色,把它放回纸箱中,搅匀后再机摸出一个球记下其颜色,把它放回纸箱中,多次重复后,发现摸到红球的频率逐渐稳定在0.2,由此可以估计纸箱中红球的个数约是20个.分析 因为摸到红球的频率在0.2附近波动,所以摸出红球的概率为0.2,再设出红球的个数,根据概率公式列方程解答即可.
解答 解:设红球的个数为x,
∵红球的频率在0.2附近波动,
∴摸出红球的概率为0.2,即$\frac{x}{100}$=0.2,
解得x=20.
所以可以估计红球的个数为20,
故答案为:20.
点评 本题考查了利用频率估计概率,大量反复试验时,某事件发生的频率会稳定在某个常数的附近,这个常数就叫做事件概率的估计值.关键是根据黑球的频率得到相应的等量关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.把一个棱长2分米的正方体木块削成一个最大的圆柱体,体积是( )立方分米.
| A. | 3.14 | B. | 12.56 | C. | 8 | D. | 6.28 |
18. 如图,△ABC以点C为旋转中心,旋转后得到△EDC,已知AB=1.5,BC=4,AC=5,则DE=( )
如图,△ABC以点C为旋转中心,旋转后得到△EDC,已知AB=1.5,BC=4,AC=5,则DE=( )
 如图,△ABC以点C为旋转中心,旋转后得到△EDC,已知AB=1.5,BC=4,AC=5,则DE=( )
如图,△ABC以点C为旋转中心,旋转后得到△EDC,已知AB=1.5,BC=4,AC=5,则DE=( )| A. | 1.5 | B. | 3 | C. | 4 | D. | 5 |
2.已知⊙O的半径为5,A为线段OP的中点,若OP=8,则点A与⊙O的位置关系是( )
| A. | 点A在⊙O内 | B. | 点A在⊙O上 | C. | 点A在⊙O外 | D. | 不确定 |
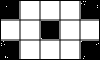 一只小狗跳来跳去,然后随意落在如图所示的某一方格中(每个方格除颜色外完全相同),则小狗停留在黑色方格中的概率是$\frac{1}{3}$.
一只小狗跳来跳去,然后随意落在如图所示的某一方格中(每个方格除颜色外完全相同),则小狗停留在黑色方格中的概率是$\frac{1}{3}$.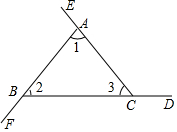 用两种方法证明“三角形的外角和等于360°”如图,∠BAE、∠CBF、∠ACD是△ABC的三个外角.
用两种方法证明“三角形的外角和等于360°”如图,∠BAE、∠CBF、∠ACD是△ABC的三个外角. 如图,已知线段AB和CD的公共部分BD=$\frac{1}{4}$CD=$\frac{1}{5}$AB,点E,F分别是AB,CD的中点,且EF=14,求AB,CD的长.
如图,已知线段AB和CD的公共部分BD=$\frac{1}{4}$CD=$\frac{1}{5}$AB,点E,F分别是AB,CD的中点,且EF=14,求AB,CD的长.