Question

10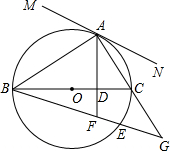．如图，BC是⊙O的直径，点A在⊙O上，AD⊥BC，垂足为D，$\underset{\widehat{AB}}{\;}$=$\widehat{AE}$，BE分别交AD、AC延长线于点F、G．
（1）判断△FAG的形状，并说明理由；
（2）过点A作直线MN，使得MN∥BG，判断直线MN与⊙O的位置关系，并说明理由．

Answer 1

分析 （1）根据圆周角定理得出∠BAC=90°，进而得出∠ACB=∠ABE，∠G=∠CAD，即可得出答案；
（2）根据平行线的性质得到∠NAG=∠G，等量代换得到∠NAG=∠FAG，∠NAC=∠BAO，求得OA⊥MN，即可得到结论．

解答 （1）证明：∵BC是⊙O的直径，
∴∠BAC=90°，
则∠G+∠ABE=90°，
∵AD⊥BC，
∴∠CAD+∠ACB=90°，
∵$\widehat{AB}$=$\widehat{AE}$，
∴∠ACB=∠ABE，
∴∠G=∠CAD，
∴AF=FG，
∴△FAG是等腰三角形；
（2）解：直线MN与⊙O相切，
理由：∵MN∥BG，
∴∠NAG=∠G，
∴∠NAG=∠FAG，∵∠BAC=ADC=90°，
∴∠CAD=∠ABO，
∵OA=OB，
∴∠OAB=∠ABO，
∴∠CAD=∠BAO，
∴∠NAC=∠BAO，
∵∠BAO+∠OAC=90°，
∴∠NAC+∠OAC=90°，
∴OA⊥MN，
∴直线MN与⊙O相切．

点评 本题考查了直线与圆的位置关系，等腰三角形的判定与性质，平行线的性质，圆周角定理，正确的作出辅助线是解题的关键．