题目内容
11.已知矩形的对角线与一条边的夹角为60°,这条边的边长为16cm,求:①矩形的对角线的长;
②矩形的面积.
分析 ①首先根据题意画出图形,然后由矩形的对角线与一条边的夹角为60°,这条边的边长为16cm,可得∠ACB=30°,继而求得矩形的对角线的长;
②首先由勾股定理求得BC的长,继而求得矩形的面积.
解答  解:①如图,∵四边形ABCD是矩形,
解:①如图,∵四边形ABCD是矩形,
∴∠B=90°,
∵∠BAC=60°,AB=16cm,
∴∠ACB=30°,
∴AC=2AB=32(cm),
即矩形的对角线的长为32cm;
②在Rt△ABC中,BC=$\sqrt{A{C}^{2}-A{B}^{2}}$=$\sqrt{3{2}^{2}-1{6}^{2}}$=16$\sqrt{3}$(cm),
∴S矩形ABCD=AB•BC=16×16$\sqrt{3}$=256$\sqrt{3}$(cm2),
即矩形的面积为:256$\sqrt{3}$cm2.
点评 此题考查了矩形的性质、含30°角的直角三角形的性质以及勾股定理.注意根据题意画出图形,结合图形求解是关键.

练习册系列答案
相关题目
6.某旅行社拟在暑假期间面向学生推出“林州红旗渠一日游”活动,收费标准如下:
甲、乙两所学校计划组织本校学生自愿参加此项活动,已知甲校报名参加的学生人数多于100人,乙校报名参加的学生人数少于100人.经核算,若两校分别组团共需花费20800元,若两校联合组团只需花费18000元.
(1)两所学校报名参加旅游的学生人数之和是多少人?
(2)两所学校报名参加旅游的学生各有多少人?
| 人数m | 0<m≤100 | 100<m≤200 | m>200 |
| 收费标准(元/人) | 90 | 85 | 75 |
(1)两所学校报名参加旅游的学生人数之和是多少人?
(2)两所学校报名参加旅游的学生各有多少人?
 为了方便行人推车过天桥,某相关部门在10m高的天桥两端修建了40m长的斜道(如图),求这条斜道的坡角α(精确到1′).
为了方便行人推车过天桥,某相关部门在10m高的天桥两端修建了40m长的斜道(如图),求这条斜道的坡角α(精确到1′). 如图,在△ABC中,DE∥BC,EF∥CD,求证:$\frac{AF}{AD}=\frac{AD}{AB}$.
如图,在△ABC中,DE∥BC,EF∥CD,求证:$\frac{AF}{AD}=\frac{AD}{AB}$.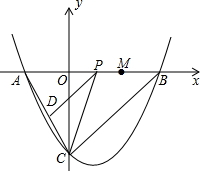 已知:如图,抛物线y=a(x-1)2+c与y轴交于点C(0,-4),与x轴交于点A、B,点A的坐标为(-2,0).
已知:如图,抛物线y=a(x-1)2+c与y轴交于点C(0,-4),与x轴交于点A、B,点A的坐标为(-2,0).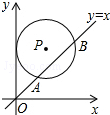 如图,在平面直角坐标系中,⊙P的圆心是(3,a)(a>3),⊙P与y轴相切,函数y=x的图象被⊙P截得的弦AB的长为2$\sqrt{5}$,则a的值是2$\sqrt{2}$+3.
如图,在平面直角坐标系中,⊙P的圆心是(3,a)(a>3),⊙P与y轴相切,函数y=x的图象被⊙P截得的弦AB的长为2$\sqrt{5}$,则a的值是2$\sqrt{2}$+3.