题目内容
18.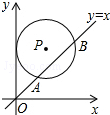 如图,在平面直角坐标系中,⊙P的圆心是(3,a)(a>3),⊙P与y轴相切,函数y=x的图象被⊙P截得的弦AB的长为2$\sqrt{5}$,则a的值是2$\sqrt{2}$+3.
如图,在平面直角坐标系中,⊙P的圆心是(3,a)(a>3),⊙P与y轴相切,函数y=x的图象被⊙P截得的弦AB的长为2$\sqrt{5}$,则a的值是2$\sqrt{2}$+3.
分析 作PH⊥y轴于H,PC⊥AB于C,作PE⊥x轴于E交AB于D,如图,先根据切线的性质得PH=2,即⊙P的半径为2,再根据垂径定理,由PC⊥AB得到BC=CD=$\frac{1}{2}$AB=$\sqrt{5}$,接着在Rt△BPC中利用勾股定理可计算出PC=1,由直线y=x为第一、三象限的角平分线得到∠DOE=45°,则∠ODE=45°,DE=OE=2,然后判断△PCD为等腰直角三角形得到PD=$\sqrt{2}$PC=2$\sqrt{2}$,所以PE=PD+DE=2$\sqrt{2}$+3,即a=2$\sqrt{2}$+3.
解答  解:作PH⊥y轴于H,PC⊥AB于C,作PE⊥x轴于E交AB于D,如图,
解:作PH⊥y轴于H,PC⊥AB于C,作PE⊥x轴于E交AB于D,如图,
∵⊙P与y轴相切,
∴PH=2,即⊙P的半径为2,
∵PC⊥AB,
∴BC=CD=$\frac{1}{2}$AB=$\frac{1}{2}$×2$\sqrt{5}$=$\sqrt{5}$,
在Rt△BPC中,PC=$\sqrt{{PB}^{2}-{BC}^{2}}$=$\sqrt{{3}^{2}-{(\sqrt{5})}^{2}}$=2,
∵直线y=x为第一、三象限的角平分线,
∴∠DOE=45°,
∴∠ODE=45°,DE=OE=3,
∴∠PDC=45°,
∴PD=$\sqrt{2}$PC=2$\sqrt{2}$,
∴PE=PD+DE=2$\sqrt{2}$+3.
故答案为:2$\sqrt{2}$+3.
点评 本题考查的是垂径定理,根据题意作出辅助线,构造出等腰直角三角形是解答此题的关键.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
3.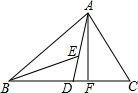 如图,在△ABC中,AD,AF分别为△ABC的中线和高,BE为△ABD的角平分线.
如图,在△ABC中,AD,AF分别为△ABC的中线和高,BE为△ABD的角平分线.
(1)若∠BED=40°,∠BAD=25°,求∠BAF的大小;
(2)若△ABC的面积为40,BD=5,求AF的长.
 如图,在△ABC中,AD,AF分别为△ABC的中线和高,BE为△ABD的角平分线.
如图,在△ABC中,AD,AF分别为△ABC的中线和高,BE为△ABD的角平分线.(1)若∠BED=40°,∠BAD=25°,求∠BAF的大小;
(2)若△ABC的面积为40,BD=5,求AF的长.
10.已知a,b,c是△ABC的三边长,其中a,b是二元一次方程组$\left\{\begin{array}{l}{a+b=10}\\{2a+b=16}\end{array}\right.$的解,那么c的值可能是下面四个数中的( )
| A. | 2 | B. | 6 | C. | 10 | D. | 18 |
7.计算:-(-1)2015的结果是( )
| A. | 1 | B. | -1 | C. | 2015 | D. | -2015 |
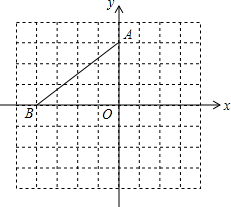 在平面直角坐标系中,点A的坐标是(0,3),点B在x轴上,将△AOB绕点A逆时针旋转90°得到△AEF,点O,B对应点分别是E,F.
在平面直角坐标系中,点A的坐标是(0,3),点B在x轴上,将△AOB绕点A逆时针旋转90°得到△AEF,点O,B对应点分别是E,F. 如图,若要使图中平面展开图折叠成正方体后,相对面上两个数字之和为6,则x-y=-10.
如图,若要使图中平面展开图折叠成正方体后,相对面上两个数字之和为6,则x-y=-10.