题目内容
20. 如图,点C把线段AB分成两条线段AC和BC(AC>BC),如果$\frac{AC}{AB}$=$\frac{BC}{AC}$,那么称线段AB被点C黄金分割,AC与AB的比叫做黄金比,其比值是$\frac{\sqrt{5}-1}{2}$.
如图,点C把线段AB分成两条线段AC和BC(AC>BC),如果$\frac{AC}{AB}$=$\frac{BC}{AC}$,那么称线段AB被点C黄金分割,AC与AB的比叫做黄金比,其比值是$\frac{\sqrt{5}-1}{2}$.
分析 设AB=1,AC=x,根据黄金分割的概念列出比例式,得到一元二次方程,解方程得到答案.
解答 解:设AB=1,AC=x,则BC=1-x,
由$\frac{AC}{AB}$=$\frac{BC}{AC}$得AC2=AB•CB,
则x2=1×(1-x)
整理得;x2+x-1=0,
解得:x1=$\frac{\sqrt{5}-1}{2}$,x2=$\frac{-\sqrt{5}-1}{2}$(不合题意,舍去).
故答案为:$\frac{\sqrt{5}-1}{2}$.
点评 本题考查的是黄金分割,理解黄金分割的概念,找出黄金分割中成比例的对应线段是解决问题的关键,注意方程思想的正确运用.

练习册系列答案
相关题目
10. 如图,身高为1.6m的某学生想测量一棵大树的高度,她沿着树影BA由B到A走去,当走到C点时,她的影子顶端正好与树的影子顶端重合,测得BC=4m,CA=1m,则树的高度为( )
如图,身高为1.6m的某学生想测量一棵大树的高度,她沿着树影BA由B到A走去,当走到C点时,她的影子顶端正好与树的影子顶端重合,测得BC=4m,CA=1m,则树的高度为( )
 如图,身高为1.6m的某学生想测量一棵大树的高度,她沿着树影BA由B到A走去,当走到C点时,她的影子顶端正好与树的影子顶端重合,测得BC=4m,CA=1m,则树的高度为( )
如图,身高为1.6m的某学生想测量一棵大树的高度,她沿着树影BA由B到A走去,当走到C点时,她的影子顶端正好与树的影子顶端重合,测得BC=4m,CA=1m,则树的高度为( )| A. | 4.8m | B. | 6.4m | C. | 8m | D. | 10m |
12.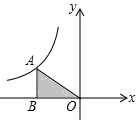 如图所示,S△ABO=2,则反比例函数的解析式是( )
如图所示,S△ABO=2,则反比例函数的解析式是( )
 如图所示,S△ABO=2,则反比例函数的解析式是( )
如图所示,S△ABO=2,则反比例函数的解析式是( )| A. | $y=-\frac{2}{x}$ | B. | $y=\frac{2}{x}$ | C. | $y=-\frac{4}{x}$ | D. | $y=\frac{4}{x}$ |
9.下列每组数据中的三个数值分别为三角形的三边长,不能构成直角三角形是( )
| A. | 4,6,8 | B. | 9,40,41 | C. | 5,12,13 | D. | 7,24,25 |
 如图,△ABC中,AC=BC,AC⊥BC,E为△ABC外一点,且∠CEA=45°,求证:AE⊥BE.
如图,△ABC中,AC=BC,AC⊥BC,E为△ABC外一点,且∠CEA=45°,求证:AE⊥BE. 某台风中心在A城正南方向100km处,以20km/h的速度向A城移动,此时一辆汽车从A城以60km/h的速度向正西方向行驶.则这辆汽车与台风中心的最近距离为30$\sqrt{10}$km.
某台风中心在A城正南方向100km处,以20km/h的速度向A城移动,此时一辆汽车从A城以60km/h的速度向正西方向行驶.则这辆汽车与台风中心的最近距离为30$\sqrt{10}$km.