如图.身高为1.6m的某学生想测量一棵大树的高度.她沿着树影BA由B到A走去.当走到C点时.她的影子顶端正好与树的影子顶端重合.测得BC=4m.CA=1m.则树的高度为( )A．4.8mB．6.4mC．8mD．10m 题目和参考答案——青夏教育精英家教网—

题目内容

10．

如图，身高为1.6m的某学生想测量一棵大树的高度，她沿着树影BA由B到A走去，当走到C点时，她的影子顶端正好与树的影子顶端重合，测得BC=4m，CA=1m，则树的高度为（　　）

A．

4.8m

B．

6.4m

C．

D．

10m

分析根据题意得出△ACD∽△ABE，再利用相似三角形的性质得出答案．

解答解：如图所示：由题意可得，CD∥BE，
则△ACD∽△ABE，
故$\frac{AC}{AB}$=$\frac{CD}{BE}$，
即$\frac{1}{5}$=$\frac{1.6}{BE}$，
解得：BE=8m．
故选：C．

点评此题主要考查了相似三角形的应用，正确利用平行线得出相似三角形是解题关键．

练习册系列答案

相关题目

20．

如图，抛物线y=-x²+bx+c经过坐标原点，并与x轴相交于点A（2，0）．
（1）求此抛物线的解析式；
（2）求抛物线顶点坐标及对称轴．

1．若$\sqrt{（x-6{）^2}}=6-x$，则x的取值范围是（　　）

18．

如图，长方形的长和宽分别是7cm和3cm，分别绕着它的长和宽所在的直线旋转一周，回答下列问题：
（1）如图（1），绕着它的宽所在的直线旋转一周，所得到的是什么样的几何体？得到的几何体的体积是多少？（π取3.14）
（2）如图（2），绕着它的长所在的直线旋转一周，所得到的是什么样的几何体？得到的几何体的体积是多少？（π取3.14）

15．

如图，在△ABC中，∠BAC=80°，∠B=40°，AD是△ABC的角平分线，求∠ADB等于多少度？

2．化简求值．
（1）（a-3b）（2a+b）+（a+2b）（2b-a），其中a=1，b=-1
（2）y（x+y）+（x+y）（x-y）-x²，其中x=-2，y=$\frac{1}{2}$．

19．

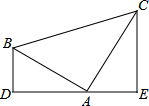如图，Rt△ABC中，∠BAC=90°，AB=AC，分别过点B，C作过点A的直线的垂线BD，CE，垂足分别为点D，E．若BD=2，CE=3，则AE=2，AD=3．

20．

如图，点C把线段AB分成两条线段AC和BC（AC＞BC），如果$\frac{AC}{AB}$=$\frac{BC}{AC}$，那么称线段AB被点C黄金分割，AC与AB的比叫做黄金比，其比值是$\frac{\sqrt{5}-1}{2}$．

试题分类