题目内容
3.已知二次函数y=ax2+bx+c的图象经过点(-2,4),(-1,0),(0,-2)(1)求这个二次函数的表达式;
(2)求此二次函数的顶点坐标及与坐标轴的交点坐标,并根据这些点画出函数大致图象;
(3)若0<y<3,求x的取值范围.
分析 (1)由题意抛物线y=ax2+bx+c(a≠0)经过(-2,4),(-1,0),(0,-2)三点,把三点代入函数的解析式,根据待定系数法求出函数的解析式;
(2)把求得的解析式化为顶点式,从而求出其对称轴和顶点坐标;分别令x=0,y=0,得到方程,解方程从而求出抛物线与坐标轴的交点坐标;
(3)把y=3代入解析式求得横坐标,从而求出x的取值范围.
解答 解:(1)∵抛物线经过(-2,4),(-1,0),(0,-2)三点,则$\left\{\begin{array}{l}{4a-2b+c=4}\\{a-b+c=0}\\{c=-2}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=1}\\{b=-1}\\{c=-2}\end{array}\right.$
∴y=x2-x-2;
(2)∵y=x2-x-2=(x-$\frac{1}{2}$)2-$\frac{9}{4}$
∴对称轴为直线x=$\frac{1}{2}$,顶点坐标为($\frac{1}{2}$,-$\frac{9}{4}$);
∵x=0,y=-2,
∴抛物线与y轴的交点坐标为(0,-2)
∵y=0,
∴x2-x-2=0,
∴x1=2,x2=-1,
∴抛物线与x轴的交点坐标为(2,0)、(-1,0).
画出函数图象如图:
(3)把y=3代入得,x2-x-2=3,解得x=$\frac{1±\sqrt{21}}{2}$
∴$\frac{1-\sqrt{21}}{2}$<x<-1 或 2<x<$\frac{1+\sqrt{21}}{2}$.
点评 本题考查了待定系数法求二次函数解析式,二次函数的性质,待定系数法求函数解析式是常用的方法,需熟练掌握并灵活运用,(2)整理成顶点式形式求解更简便.

 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案| A. | -4 | B. | -4 | C. | 0 | D. | -6 |
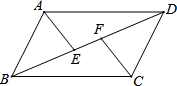 如图,AB=CD,AB∥CD,E,F是BD上两点且BE=DF,则图中全等的三角形有( )
如图,AB=CD,AB∥CD,E,F是BD上两点且BE=DF,则图中全等的三角形有( )| A. | 1对 | B. | 2对 | C. | 3对 | D. | 4对 |
 如图,点C把线段AB分成两条线段AC和BC(AC>BC),如果$\frac{AC}{AB}$=$\frac{BC}{AC}$,那么称线段AB被点C黄金分割,AC与AB的比叫做黄金比,其比值是$\frac{\sqrt{5}-1}{2}$.
如图,点C把线段AB分成两条线段AC和BC(AC>BC),如果$\frac{AC}{AB}$=$\frac{BC}{AC}$,那么称线段AB被点C黄金分割,AC与AB的比叫做黄金比,其比值是$\frac{\sqrt{5}-1}{2}$.
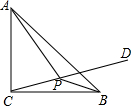 如图,已知△ABC为等腰直角三角形,AC=BC=4,∠BCD=15°,P为CD上的动点,则|PA-PB|的最大值是( )
如图,已知△ABC为等腰直角三角形,AC=BC=4,∠BCD=15°,P为CD上的动点,则|PA-PB|的最大值是( ) 如图,AB、CD相交于点E,EA=EC,AC∥BD.求证:EB=ED.
如图,AB、CD相交于点E,EA=EC,AC∥BD.求证:EB=ED.