题目内容
8. 如图,△ABC中,AC=BC,AC⊥BC,E为△ABC外一点,且∠CEA=45°,求证:AE⊥BE.
如图,△ABC中,AC=BC,AC⊥BC,E为△ABC外一点,且∠CEA=45°,求证:AE⊥BE.
分析 首先过C点作CF⊥CE交BE的延长线于F,根据等腰直角三角形的性质得到∠ABC=45°,得到∠ABC=∠CEA=45°,推出A,B,E,C四点共圆,由圆周角定理得到∠CAE=∠CBE,推出△ACE≌△BCF(SAS),于是得到∠AEC=∠F=45°,即可得到结论.
解答  证明:过C点作CF⊥CE交BE的延长线于F,
证明:过C点作CF⊥CE交BE的延长线于F,
∵AC=BC,AC⊥BC,
∴∠ABC=45°,
∵∠CEA=45°,
∴∠ABC=∠CEA=45°,
∴A,B,E,C四点共圆,
∴∠CAE=∠CBE,
∵∠ACB=∠ECF,
∴∠ACE=∠BCF,
在△ACE和△BCF中,
$\left\{\begin{array}{l}{∠ACE=∠BCF}\\{AC=BC}\\{∠CAE=∠CBE}\end{array}\right.$,
∴△ACE≌△BCF(SAS),
∴∠AEC=∠F=45°,
∴∠AEF=∠AEC+∠CEF=90°,
∴∠AEB=90°,
即AE⊥BE.
点评 此题考查了全等三角形的判定与性质以及等腰三角形的性质.此题难度较大,解题的关键是准确作出辅助线.

练习册系列答案
相关题目
13.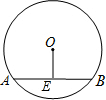 如图,已知⊙O的半径为10cm,弦AB的长为12cm,则弦AB的弦心距OE的长为( )
如图,已知⊙O的半径为10cm,弦AB的长为12cm,则弦AB的弦心距OE的长为( )
 如图,已知⊙O的半径为10cm,弦AB的长为12cm,则弦AB的弦心距OE的长为( )
如图,已知⊙O的半径为10cm,弦AB的长为12cm,则弦AB的弦心距OE的长为( )| A. | 5cm | B. | 6cm | C. | 7cm | D. | 8cm |
11.函数y=x2+x-6的图象与y轴交点的纵坐标是( )
| A. | -4 | B. | -4 | C. | 0 | D. | -6 |
 如图,长方形的长和宽分别是7cm和3cm,分别绕着它的长和宽所在的直线旋转一周,回答下列问题:
如图,长方形的长和宽分别是7cm和3cm,分别绕着它的长和宽所在的直线旋转一周,回答下列问题: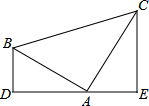 如图,Rt△ABC中,∠BAC=90°,AB=AC,分别过点B,C作过点A的直线的垂线BD,CE,垂足分别为点D,E.若BD=2,CE=3,则AE=2,AD=3.
如图,Rt△ABC中,∠BAC=90°,AB=AC,分别过点B,C作过点A的直线的垂线BD,CE,垂足分别为点D,E.若BD=2,CE=3,则AE=2,AD=3. 如图,AB=CD,AD=CB,求证:∠A=∠C.小丽的思考过程如下:∵$\left\{\begin{array}{l}{AB=CD}\\{AO=CO}\\{BO=OD}\end{array}\right.$,∴△ABO≌△CDO,∴∠A=∠C
如图,AB=CD,AD=CB,求证:∠A=∠C.小丽的思考过程如下:∵$\left\{\begin{array}{l}{AB=CD}\\{AO=CO}\\{BO=OD}\end{array}\right.$,∴△ABO≌△CDO,∴∠A=∠C 如图,在△ABC中,∠ABC=2∠C,AD是∠BAC的平分线,求证:AB+BD=AC.
如图,在△ABC中,∠ABC=2∠C,AD是∠BAC的平分线,求证:AB+BD=AC. 如图,点C把线段AB分成两条线段AC和BC(AC>BC),如果$\frac{AC}{AB}$=$\frac{BC}{AC}$,那么称线段AB被点C黄金分割,AC与AB的比叫做黄金比,其比值是$\frac{\sqrt{5}-1}{2}$.
如图,点C把线段AB分成两条线段AC和BC(AC>BC),如果$\frac{AC}{AB}$=$\frac{BC}{AC}$,那么称线段AB被点C黄金分割,AC与AB的比叫做黄金比,其比值是$\frac{\sqrt{5}-1}{2}$.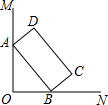 如图,∠MON=90°,矩形ABCD的顶点A、B分别在边OM,ON上,当B在边ON上运动时,A随之在边OM上运动,矩形ABCD的形状保持不变,其中AB=8,BC=3,运动过程中,点D到点O的最大距离为9.
如图,∠MON=90°,矩形ABCD的顶点A、B分别在边OM,ON上,当B在边ON上运动时,A随之在边OM上运动,矩形ABCD的形状保持不变,其中AB=8,BC=3,运动过程中,点D到点O的最大距离为9.