题目内容
18.定义符号min[a,b]的含义为:当a≥b时,min[a,b]=b;当a<b时,min[a,b]=a,如min[1,-2]=-2,min[-1,2]=-1.已知当-$\frac{1}{2}$≤x≤2时,min[x2-2x-3,k(x-1)]=x2-2x-3,则k的取值范围是-3<k<$\frac{7}{6}$.分析 根据当-$\frac{1}{2}$≤x≤2时,y=x2-2x-3的值小于y=k(x-1)的值,解答即可.
解答 解:对于y=x2-2x-3,当x=-$\frac{1}{2}$时,y=-$\frac{7}{4}$,当x=2时,y=-3,
由题意可知抛物线y=x2-2x-3与直线y=k(x-1)的交点坐标为(-$\frac{1}{2}$,-$\frac{7}{4}$),(2,-3),
所以k的范围是:-3<k<$\frac{7}{6}$,
故答案为-3<k<$\frac{7}{6}$.
点评 本题考查的是与二次函数和一次函数有关的新定义,根据题意理解新定义的计算公式是解题的关键,注意:一次函数和二次函数的性质的运用.

练习册系列答案
相关题目
20.经专家估算,南海属我国传统疆线以内的油气资源约合15 000亿美元,用科学记数法表示数字15 000是( )
| A. | 15×10 3 | B. | 1.5×10 3 | C. | 1.5×10 4 | D. | 1.5×10 5 |
9.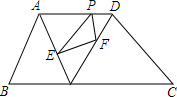 已知,在面积为7的梯形ABCD中,AD∥BC,AD=3,BC=4,P为边AD上不与A、D重合的一动点,Q是边BC上的任意一点,连结AQ、DQ,过P作PE∥DQ交AQ于E,作PF∥AQ交DQ于F.则△PEF面积的最大值是( )
已知,在面积为7的梯形ABCD中,AD∥BC,AD=3,BC=4,P为边AD上不与A、D重合的一动点,Q是边BC上的任意一点,连结AQ、DQ,过P作PE∥DQ交AQ于E,作PF∥AQ交DQ于F.则△PEF面积的最大值是( )
 已知,在面积为7的梯形ABCD中,AD∥BC,AD=3,BC=4,P为边AD上不与A、D重合的一动点,Q是边BC上的任意一点,连结AQ、DQ,过P作PE∥DQ交AQ于E,作PF∥AQ交DQ于F.则△PEF面积的最大值是( )
已知,在面积为7的梯形ABCD中,AD∥BC,AD=3,BC=4,P为边AD上不与A、D重合的一动点,Q是边BC上的任意一点,连结AQ、DQ,过P作PE∥DQ交AQ于E,作PF∥AQ交DQ于F.则△PEF面积的最大值是( )| A. | $\frac{3}{2}$ | B. | $\frac{3}{8}$ | C. | $\frac{1}{4}$ | D. | $\frac{3}{4}$ |
 如图,在△ABC中,∠A=120°,点D是BC的中点,点E是AB上的一点,点F是AC上的一点,∠EDF=90°,且BE=2,FC=7,则EF=$\sqrt{39}$.
如图,在△ABC中,∠A=120°,点D是BC的中点,点E是AB上的一点,点F是AC上的一点,∠EDF=90°,且BE=2,FC=7,则EF=$\sqrt{39}$. 在梯形ABCD中,AB∥CD,AC、BD交于点E,AD、BC的延长线交于点H,过点E作FG∥AB交AD于点F,交BC于点G,求证:AG、BF、EH三线共点.
在梯形ABCD中,AB∥CD,AC、BD交于点E,AD、BC的延长线交于点H,过点E作FG∥AB交AD于点F,交BC于点G,求证:AG、BF、EH三线共点. 如图,在四边形ABCD中,∠ABC=90°,AB=1,BC=2,CD=2,AD=3,连接AC,试判断△ACD的形状.
如图,在四边形ABCD中,∠ABC=90°,AB=1,BC=2,CD=2,AD=3,连接AC,试判断△ACD的形状.