题目内容
5.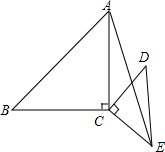 如图,AC=BC,DC=EC,且AC⊥BC,DC⊥EC.求证:
如图,AC=BC,DC=EC,且AC⊥BC,DC⊥EC.求证:(1)AE=BD;
(2)AE⊥BD;
(3)∠AEC=∠BDC.
分析 (1)连接BD,由AC⊥BC,DC⊥EC,得到∠ACB=∠DCE=90°,证得∠BCD=∠ACE,得到△BCD≌△ACE,于是证得AE=BD;
(2)由(1)证得△BCD≌△ACE,得到∠DBC=∠ECA,通过等量代换得到AE⊥BD;
(3)由(1)证得△BCD≌△ACE,得到∠AEC∠=∠BDC.
解答 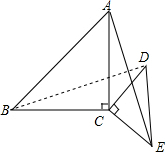 证明:(1)连接BD,
证明:(1)连接BD,
∵AC⊥BC,DC⊥EC,
∴∠ACB=∠DCE=90°,
∴∠ACB+∠ACD=∠DCE+∠ACD,
即∠BCD=∠ACE,
在△BCD与△ACE中,$\left\{\begin{array}{l}{BC=AC}\\{∠BCD=∠ACE}\\{CD=CE}\end{array}\right.$,
∴△BCD≌△ACE,
∴AE=BD;
(2)由(1)证得△BCD≌△ACE,
∴∠DBC=∠ECA,
∵∠ABD+∠DBC+∠BAC=90°,
∴∠ABD+∠CAD+∠BAC=90°,
∴AE⊥BD;
(3)由(1)证得△BCD≌△ACE,
∴∠AEC∠=∠BDC.
点评 本题考查了全等三角形的判定与性质,垂直的定义,掌握定理是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

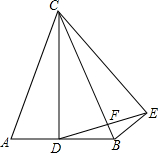 已知AC=BC,DC=EC,∠BCA=∠DCE,CD⊥AB,求证:∠BCE=∠BEF.
已知AC=BC,DC=EC,∠BCA=∠DCE,CD⊥AB,求证:∠BCE=∠BEF.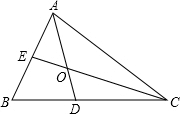 如图,在△ABC中,∠B=60°,∠BAC、∠BCA的平分线AD,CE交于点O,猜想OE与OD的大小关系和AC与AE、CD的大小关系,并说出你的理由.
如图,在△ABC中,∠B=60°,∠BAC、∠BCA的平分线AD,CE交于点O,猜想OE与OD的大小关系和AC与AE、CD的大小关系,并说出你的理由.