题目内容
17.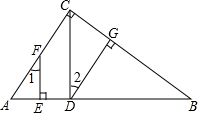 已知,如图,DG⊥BC,AC⊥BC,EF⊥AB,∠1=∠2,求证:CD⊥AB.
已知,如图,DG⊥BC,AC⊥BC,EF⊥AB,∠1=∠2,求证:CD⊥AB.证明:∵DG⊥BC,AC⊥BC,(已知)
∴DG∥AC(同位角相等,两直线平行)
∴∠2=∠ACD(两直线平行,内错角相等)
∵∠1=∠2(已知)
∴∠1=∠DCA(等量代换)
∴EF∥CD(同位角相等,两直线平行)
∴∠AFE=∠ADC(两直线平行,同位角相等)
∵EF⊥AB(已知)
∴∠AEF=90°(垂直定义)
∴∠ADC=90°(等量代换)
∴CD⊥AB(垂直定义)
分析 首先证明∠2=∠DCA,然后根据∠1=∠2,可得∠DCA=∠1,再根据同位角相等,两直线平行可判定出EF∥DC,然后根据∠AFE=∠ADC,∠AEF=90°,得出∠ADC=90°.
解答 证明:∵DG⊥BC,AC⊥BC,(已知)
∴DG∥AC(同位角相等,两直线平行 )
∴∠2=∠ACD ( 两直线平行,内错角相等 )
∵∠1=∠2(已知)
∴∠1=∠DCA(等量代换)
∴EF∥CD(同位角相等,两直线平行)
∴∠AEF=∠ADC(两直线平行,同位角相等)
∵EF⊥AB(已知)
∴∠AEF=90°(垂直定义)
∴∠ADC=90°(等量代换)
∴CD⊥AB(垂直定义)
故答案为同位角相等,两直线平行;∠ACD; 两直线平行,内错角相等;两直线平行,同位角相等;垂直定义.
点评 此题主要考查了平行线的判定与性质定理,关键是掌握平行线的判定是由角的数量关系判断两直线的位置关系.平行线的性质是由平行关系来寻找角的数量关系.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
7.将△ABC三个顶点横坐标都乘以-1,纵坐标不变,则所得图形与原图形的关系是( )
| A. | 关于x轴对称 | B. | 关于y轴对称 | C. | 关于原点对称 | D. | 不存在对称关系 |
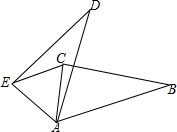 在△ABC中,∠CAB=75°,在同一平面内,将△ABC绕点A逆时针旋转到△AED的位置,使得DE∥AB,则∠DAB等于30°.
在△ABC中,∠CAB=75°,在同一平面内,将△ABC绕点A逆时针旋转到△AED的位置,使得DE∥AB,则∠DAB等于30°.