题目内容
2.已知梯形ABCD,AD∥BC,AC与BD交于点O,过点O作EF∥AD分别交AB、CD于点E、F.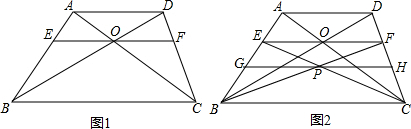
(1)如图1,求证:OE=OF;
(2)如图1,若BC-AD=7,EF-AD=3,求AD的长;
(3)如图2,联结BF、CE交于点P,过点P作GH∥BC分别交AB、CD于点G、H,求证:$\frac{1}{AD}$+$\frac{2}{BC}$=$\frac{1}{EF}$+$\frac{2}{GH}$.
分析 (1)根据AD∥BC,EF∥AD可得出△BOE∽△BDA,△AEO∽△ABC,△DOF∽△DOB,由相似三角形的对应边成比例即可得出结论;
(2)根据(1)可知,$\frac{EO}{BC}$=$\frac{AE}{AB}$,$\frac{EO}{AD}$=$\frac{BE}{AB}$,故$\frac{EO}{BC}$+$\frac{EO}{AD}$=1,$\frac{1}{BC}$+$\frac{1}{AD}$=$\frac{1}{EO}$=$\frac{2}{EF}$.根据BC=AD+7,EF=AD+3,设AD=x,代入•上式进行计算即可;
(3)根据(1)可知$\frac{1}{AD}$+$\frac{1}{BC}$=$\frac{2}{EF}$①,同理可得$\frac{1}{EF}$+$\frac{1}{BC}$=$\frac{2}{GH}$②,再把两式相加即可.
解答 解:(1)∵AD∥BC,EF∥AD可得出△AEO∽△ABC,△DOF∽△DOB,
∴$\frac{EO}{BC}$=$\frac{AE}{AB}$=$\frac{DF}{DC}$=$\frac{OF}{BC}$,
∴OE=OF;
(2)∵由(1)知,$\frac{EO}{BC}$=$\frac{AE}{AB}$,$\frac{EO}{AD}$=$\frac{BE}{AB}$,
∴$\frac{EO}{BC}$+$\frac{EO}{AD}$=1,
∴$\frac{1}{BC}$+$\frac{1}{AD}$=$\frac{1}{EO}$=$\frac{2}{EF}$.
∵BC=AD+7,EF=AD+3,
设AD=x,则
$\frac{1}{x+7}$+$\frac{1}{x}$=$\frac{1}{x+2}$,
解得x=21.
(3)∵由(1)知$\frac{1}{AD}$+$\frac{1}{BC}$=$\frac{2}{EF}$①,
同理可得$\frac{1}{EF}$+$\frac{1}{BC}$=$\frac{2}{GH}$②,
∴①-②得$\frac{1}{AD}$+$\frac{2}{BC}$=$\frac{1}{EF}$+$\frac{2}{GH}$.
点评 本题考查的是相似形综合题,涉及到相似三角形的判定与性质、梯形的性质等知识,在解答(2)时要注意设出未知数,利用方程求解.

 如图,点A、D、G、M在半圆上,四边形ABOC、DEOF、HNMO均为矩形,设BC=a,EF=b,NH=c,则下列各式中正确的是( )
如图,点A、D、G、M在半圆上,四边形ABOC、DEOF、HNMO均为矩形,设BC=a,EF=b,NH=c,则下列各式中正确的是( )| A. | a>b>c | B. | a=b=c | C. | c>a>b | D. | b>c>a |
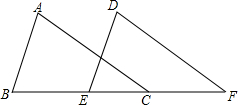 如图,在△ABC中,BC=5,∠A=70°,∠B=75°,把△ABC沿直线BC的方向平移到△DEF的位置,若CF=3,则下列结论中错误的是( )
如图,在△ABC中,BC=5,∠A=70°,∠B=75°,把△ABC沿直线BC的方向平移到△DEF的位置,若CF=3,则下列结论中错误的是( )| A. | BE=3 | B. | ∠F=35° | C. | DF=5 | D. | AB∥DE |
 在矩形ABCD中,点E在CD上,且BE平分∠AEC,若∠DAE=30°,BE=2,则AD=( )
在矩形ABCD中,点E在CD上,且BE平分∠AEC,若∠DAE=30°,BE=2,则AD=( )| A. | $\sqrt{3}$ | B. | 2 | C. | 1 | D. | $\frac{{\sqrt{3}}}{2}$ |
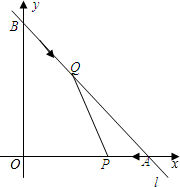 如图,已知直线l的函数表达式为y=-$\frac{4}{3}$x+8,且l与x轴、y轴分别交于A、B两点,动点Q从B点开始在线段BA上以每秒2个单位的速度向点A移动,同时动点P从A点开始在线段AO上以每秒1个单位的速度向O点移动,设点Q、P移动时间为t秒.
如图,已知直线l的函数表达式为y=-$\frac{4}{3}$x+8,且l与x轴、y轴分别交于A、B两点,动点Q从B点开始在线段BA上以每秒2个单位的速度向点A移动,同时动点P从A点开始在线段AO上以每秒1个单位的速度向O点移动,设点Q、P移动时间为t秒.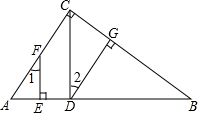 已知,如图,DG⊥BC,AC⊥BC,EF⊥AB,∠1=∠2,求证:CD⊥AB.
已知,如图,DG⊥BC,AC⊥BC,EF⊥AB,∠1=∠2,求证:CD⊥AB.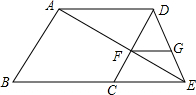 如图,已知?ABCD,点E在边BC延长线上一点,AE与CD交于点于F,FG∥BC,FG交DE于G.
如图,已知?ABCD,点E在边BC延长线上一点,AE与CD交于点于F,FG∥BC,FG交DE于G.