题目内容
已知关于多项式mx2+4xy-x-2x2+2nxy-3y合并后不含有二次项,求nm的值.
考点:合并同类项,多项式
专题:
分析:由于多项式mx2+4xy-x-2x2+2nxy-3y合并后不含有二次项,即二次项系数为0,在合并同类项时,可以得到二次项为0,由此得到故m、n的方程,即m-3=0,2n+4=0,解方程即可求出m,n,然后把m、n的值代入nm,即可求出代数式的值.
解答:解:∵多项式mx2+4xy-x-2x2+2nxy-3y合并后不含有二次项,
即二次项系数为0,
即m-2=0,
∴m=2;
∴2n+4=0,
∴n=-2,
把m、n的值代入nm中,得原式=4.
即二次项系数为0,
即m-2=0,
∴m=2;
∴2n+4=0,
∴n=-2,
把m、n的值代入nm中,得原式=4.
点评:考查了多项式,根据在多项式中不含哪一项,则哪一项的系数为0,由此建立方程,解方程即可求得待定系数的值.

练习册系列答案
相关题目
 如图,为安全起见,幼儿园打算加长滑梯,将其倾斜角由45°降至30°.已知滑梯AB的长为3m,点D,B,C在同一水平地面上,那么加长后的滑梯AD的长是多少m?
如图,为安全起见,幼儿园打算加长滑梯,将其倾斜角由45°降至30°.已知滑梯AB的长为3m,点D,B,C在同一水平地面上,那么加长后的滑梯AD的长是多少m?
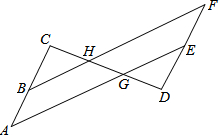 已知:如图,AC∥DF,点为线段AC上一点,连接BF交DC于点H,过点作AE∥BF分别交DC、DF于点G、点,DG=CH,求证:△DFH≌△CAG.
已知:如图,AC∥DF,点为线段AC上一点,连接BF交DC于点H,过点作AE∥BF分别交DC、DF于点G、点,DG=CH,求证:△DFH≌△CAG. 如图,在菱形ABCD中,∠ABC=120°,E是AB边上的中点,P是AC边上一动点,PB+PE的最小值是
如图,在菱形ABCD中,∠ABC=120°,E是AB边上的中点,P是AC边上一动点,PB+PE的最小值是